Velocity is a physical quantity that measures how fast an object moves along a fixed direction. Suppose a car moves along a straight line and covers 40 meters in 4 seconds. The car moves 40/4 = 10 meters per second along that straight line. So velocity is just how much an object is displaced per second or per unit time. Velocity is a vector quantity.
To understand velocity let us consider the following figure-1. An object travels from point A to point B along the path APB (red path).
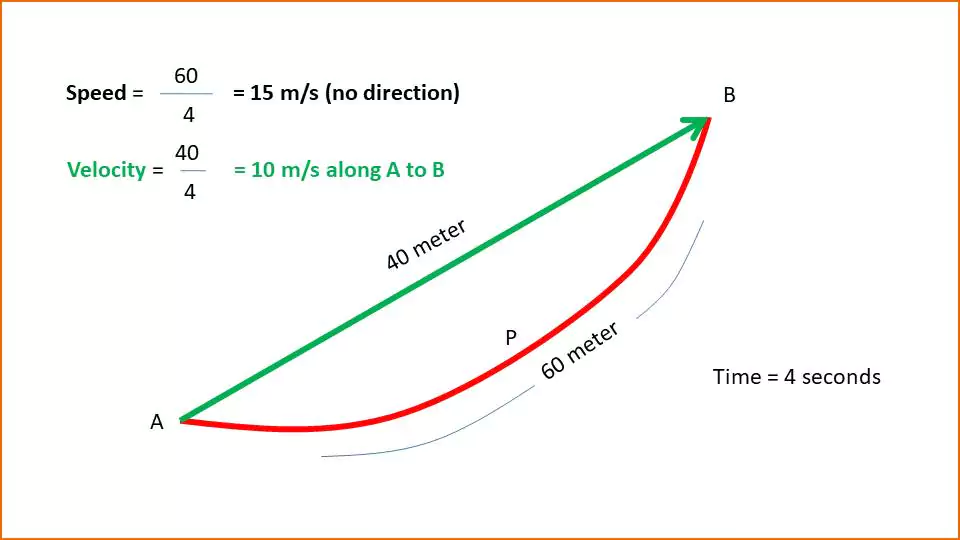
Here the time taken to reach point B by the object is 4 seconds. Though the distance covered by the object is 60 meters, its displacement is 40 meters. So the velocity is displacement/time = 40/4 = 10 m/s along points A to B. Its speed is distance/time = 60/4 = 15 m/s.
Info: The magnitude of velocity is speed.
Info: The slope of a displacement-time graph gives velocity.
Definition of velocity
The rate of change of displacement with respect to time is called velocity.
The amount of displacement per unit time is known as velocity.
Formula of Velocity
If s is the displacement of an object in time t then the formula of velocity v is –
$$\text{velocity} = \frac{\text{displacement} }{\text{time}}$$
$$\vec{v} = \frac{\vec{s} }{t}$$
Unit of Velocity:
$$\text{Unit of velocity} = \frac{\text{unit of displacement}}{\text{unit of time}}$$
- SI unit of velocity = m/s (meter per second or m.s−1)
- CGS unit of velocity = cm/s (centimeter per second or cm.s−1))
- FPS unit of velocity = ft/s (foot per second or ft.s−1)
Dimension of Velocity:
$\text{Dimension of velocity} = \frac{\text{dimension of displacement}}{\text{dimension of time}}$
$$\text{Dimension of Velocity} = \frac{[L]}{[T]}$$
$$\text{Dimension of Velocity} = [LT^{-1}]$$
Types of Velocity
Uniform Velocity:
If an object moves an equal amount of displacement in an equal interval of time, then we can say that it has uniform velocity.
If the magnitude and direction both remain the same in all instances then its velocity is uniformLet an object displaced x in time t, then displaced 2x in time 2t, and then displaced 3x in time 3t. Its velocity is said to be uniform.
Example:: A car moving at 40 km/h in a straight road without changing speed.
Non-uniform Velocity:
If an object displaces unequal distances in equal intervals of time, the velocity of the object is called non-uniform velocity.
If the magnitude of velocity or the direction or both changes with respect to time, then its velocity is non-uniform.Let an object displaced x in time t, then it displaced 2x in time t, and then it displaced 1.5x in the same interval of time t. Clearly, it covers unequal displacement (i.e. x, 2x 1.5x) in equal intervals of time. Its velocity is said to be non-uniform.
Example:: A car accelerating or moving on a curved path.
Average Velocity:
Let the displacement of an object is not equal in the equal interval of time. The velocity will not be the same for all instances. In that case we need to calculate the average velocity. The average velocity is the total displacement divided by the total time.
Average velocity is the change of total displacement (s) divided by total time (t).Mathematically,
$$\left< \vec{v}\right> = \frac{ \text {total displacement}}{\text{total time }}$$
Let a body move from point A(x1) to point B(x2) at the time interval t1 to t2 then mathematically average velocity is
$$\vec{v}_{\text{avg}} = \left< \vec{v}\right> = \frac{x_2 – x_1}{t_2 – t_1}$$
Info: Average velocity is useful when velocity is changing over time.
In the following figure-2.1, a car moves along a straight line through points A, B, C, D and E. It displaced s1 in time t1, s2 in time t2, s3 in time t3 and s4 in time t4.

So mathematically, the average Velocity $\left< \vec{v}\right>$ is –
$$\left< \vec{v}\right> = \frac{ \vec{s_1}+\vec{s_2}+\vec{s_3}+\vec{s_4}}{t_1+t_2+t_3+t_4}$$
Now let us consider an example, a person moves 5 m forward and then 3 m backward in 4 seconds, its average velocity is
$$\left< \vec{v}\right> = \frac{(5 – 3)}{4} = \frac{2}{4} = 0.5 \text{ m/s}$$
Instantaneous Velocity
The velocity of an object at a particular instant of time is called Instantaneous Velocity.To understand this let a particle displaced ΔS from point B to C (as shown in fig-2.2) at the interval of time between t to (t+Δt). Mathematically, average velocity $\left< \vec{v}\right>$ is
$$\left< \vec{v}\right> = \frac{\Delta \vec{s}}{\Delta t}$$
If we decrease the time interval, the displacement by the particle will also decrease. Also if the value of Δt tends to zero, the value of ΔS will tend to zero. In this situation, the limiting value of the average velocity is called the instantaneous velocity. Mathematically
$$\vec{v}_{\text{inst}} = \lim_{\Delta t \to 0} \frac{\Delta \vec{s}}{\Delta t}$$
or, using differentiation
$$\vec{v}_{\text{inst}} = \frac{d\vec{s}}{dt} $$
Info: The speedometer of a car shows the instantaneous velocity.
Info: Circular Motion: If an object rotates around a circular path and covers an equal amount of path in equal time, we can say that its speed is uniform. But in this case, we can not say that its velocity remains the same in all instances. Because the direction of velocity is always changing.
Velocity-Time Graph
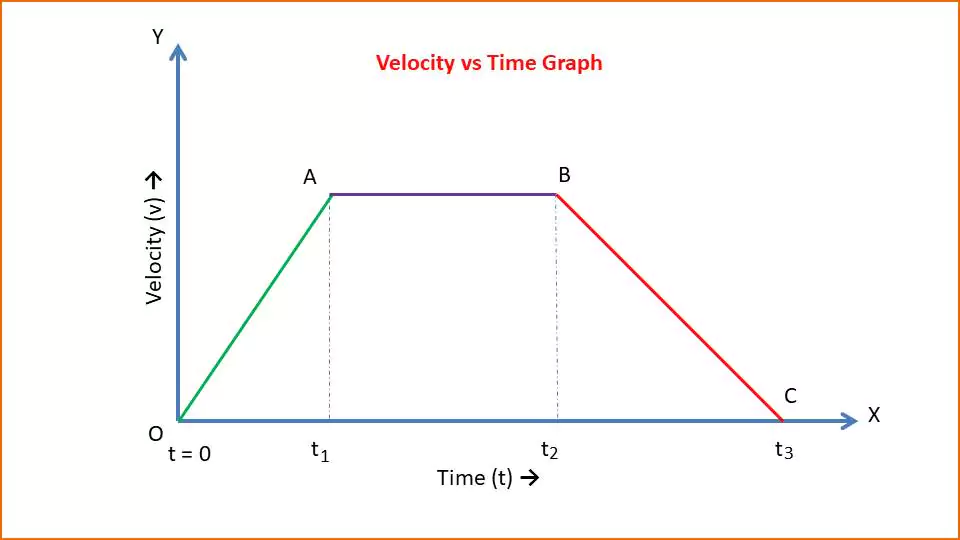
The above figure-2 shows the velocity vs time graph. The X-axis and Y-axis represent the time and speed respectively.
- At time t =0, the velocity of a particle is zero (Point O).
- At time t=0 to t1, its velocity increases with constant acceleration (OA line).
- From time t1 to t2 its velocity is constant (AB line).
- From time t2 to t3 its velocity is decreasing with constant acceleration (BC line).
- At time t3 the particle comes to rest again (Point C) velocity = 0.
The area (area of OABC) under a velocity-time graph gives the displacement.
Velocity vs. Speed
| Property | Velocity | Speed |
|---|---|---|
| Definition | Rate of change of displacement | Rate of change of distance |
| Type | Vector | Scalar |
| Formula | $\vec{v} = \frac{\Delta x}{\Delta t}$ | $s = \frac{\Delta d}{\Delta t}$ |
| Can be Negative? | Yes (depends on direction) | No (always positive) |
| Example | (1) A car moving east at 60 km/h (2) +5 m/s east | (1) A car moving at 60 km/h (without direction) (2) 5 m/s |
Problems Solutions
A car moves along a straight road, and its displacement-time graph is given by the equation: x=5t2+3t. Find the instantaneous velocity at t = 4 s.
Solution: Instantaneous velocity is given by the formula –
$$v = \frac{dx}{dt}$$
First we need to differentiate x=5t2+3t with respect to time t.
$$v = \frac{d}{dt} (5t^2 + 3t) = 10t + 3$$
Putting the value of t = 4 sec.
$$v = 10(4) + 3 = 40 + 3 = 43 \text{ m/s}$$
Find the average velocity from t=2 s to t = 4 s of the above given problem.
Solution:
The formula for average velocity is
$$ \left< \vec{v}\right> = \frac{x_2 – x_1}{t_2 – t_1}$$
At first we need to find the displacements covered at two different times i.e. at x1 at t = 2 s and x2 at t = 4 s.
$$x_2 = 5(4)^2 + 3(4) = 80 + 12 = 92 \text{ m}$$
$$x_1 = 5(2)^2 + 3(2) = 20 + 6 = 26 \text{ m}$$
putting these values in the above formula we get
$$\left< \vec{v}\right>= \frac{92 – 26}{4 – 2} = \frac{66}{2} = 33 \text{ m/s}$$