Vector Addition

Scalar quantities of the same type can be added in simple algebraic rules. For example, the masses of two objects are 20 g and 30 g respectively. Their total mass is 50 g. Multiple vector quantities of the same type can also be added. For example, force can be added to force, displacement can be added to displacement. But two vector quantities cannot be added in simple algebraic rules. This is because, both the magnitude and direction of the vector have to be considered. Multiple vectors of the same type can be added geometrically or analytically.

It is noteworthy that the magnitude of two vectors cannot be determined if they are not similar. For example, a displacement vector cannot be added to a force vector.

Resultant Vector: A vector is obtained by adding two or more vectors. If this new vector is equal to the result of the combined operation of the given vectors, then that new vector is called the resultant vector.

A resultant vector is the combined effect of adding two or more vectors.

The resultant vector is always dependent on the direction of the given vectors.

In general, the magnitude of the resultant vector is not equal to the sum of the magnitudes of the vectors involved. For example, adding a 3N force and a 4N force does not always give a 7N force.

Now let us consider the figure below.

Case-1: 3N and 4N force vectors act in the same direction. Their resultant force is 7N. In this case, as the angle between them is zero, their resultant force is obtained by adding algebraically.

Case-2: 3N and 4N forces act in the opposite direction. Their resultant force is −1N. In this case also these two force vectors follow the simple algebra. the angle between them is 180.

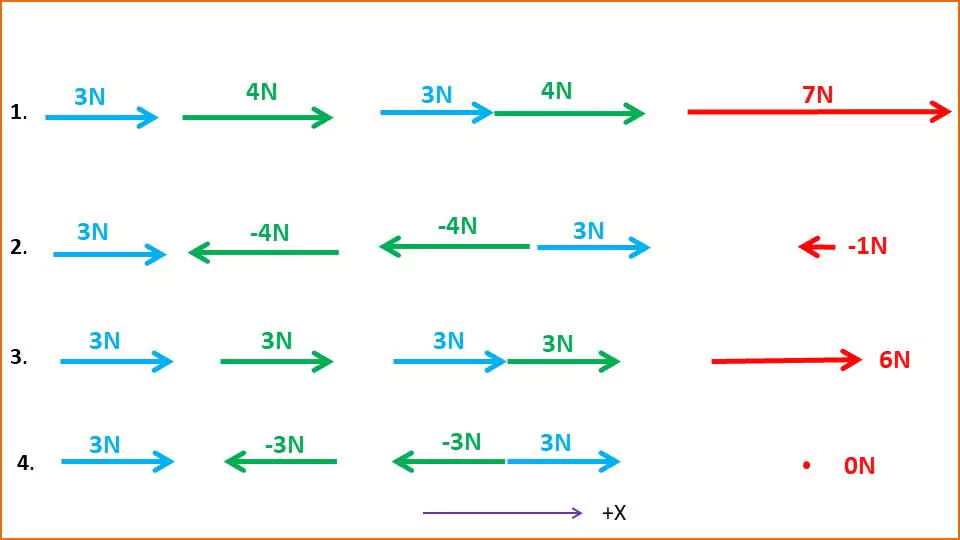
Case-3: Two equal force vectors, 3N acting in the same direction and they simply added up to give the resultant vector (6N).

Case-4: Two equal force vectors, 3N acting in the opposite direction and give the resultant vector to zero.

In all the 4 cases given above, the angle between two vectors is either 0 or 180. So the resultant vector is given by following simple algebraic rules.

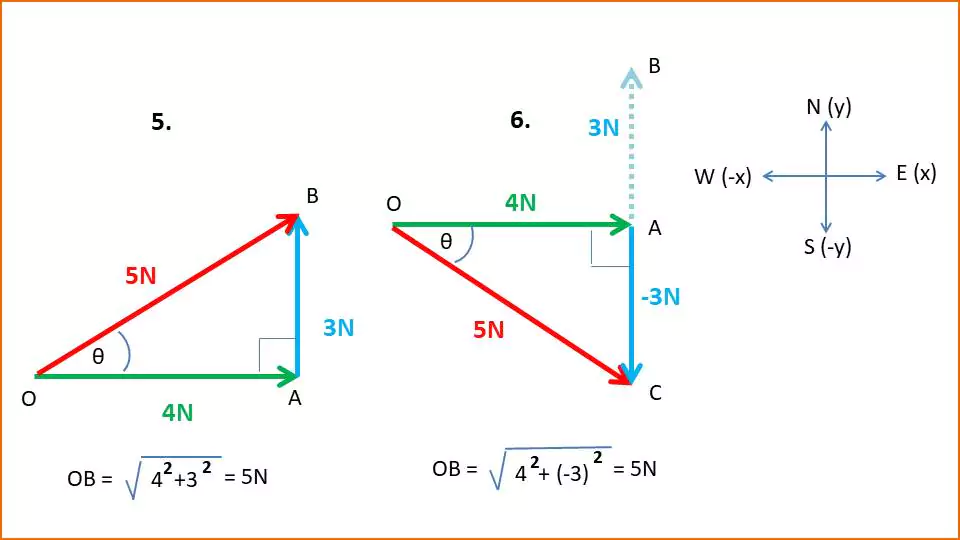
Case-5: Here 4N and 3N force vectors are acting in different directions i.e. they are making 90. In this case we can not add 4N and 3N by simple algebra. Their resultant force is 5N, not (4N + 3N) = 7N. The resultant force is given by the Pythagorean theorem.

Case-6: Here 4N and (−)3N force vectors are also making 90. So the resultant vector is 5N following the Pythagorean theorem.

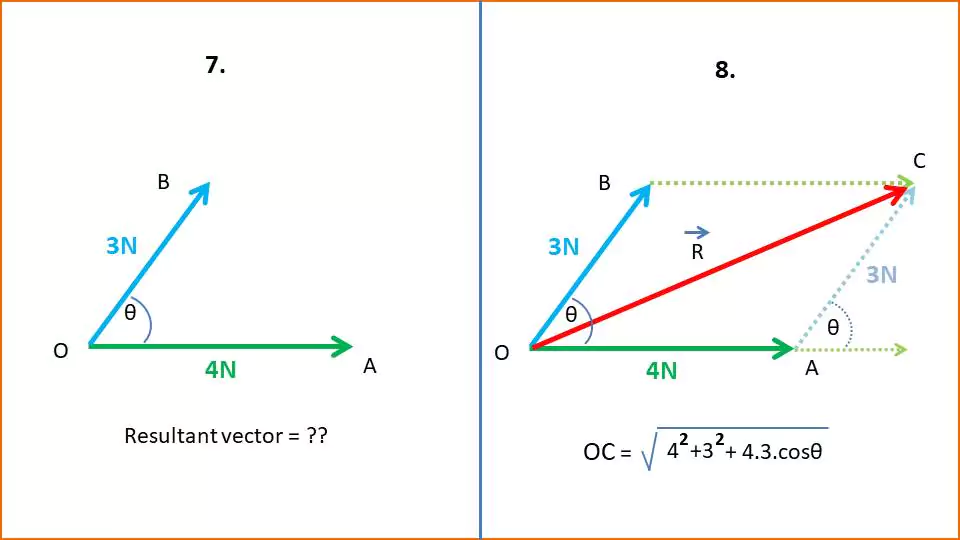
Case-7: Now what will be the resultant vector if 4N and 3N force vectors are making an angle θ? In this case two vectors can not be added by following simple algebra.

Case-8: So if two vectors make an angle, we need to follow the triangle or parallelogram rule to find the resultant vector.

We can add two vectors using 2 methods

1. Geometric Method
2. Algebraic Method (Component)

Geometric Method

Triangle law

To add two vectors geometrically (triangle law) we need to place the tail of the second vector at the head of the first vector. Then, the resultant vector is drawn from the tail of the first vector to the head of the second vector.

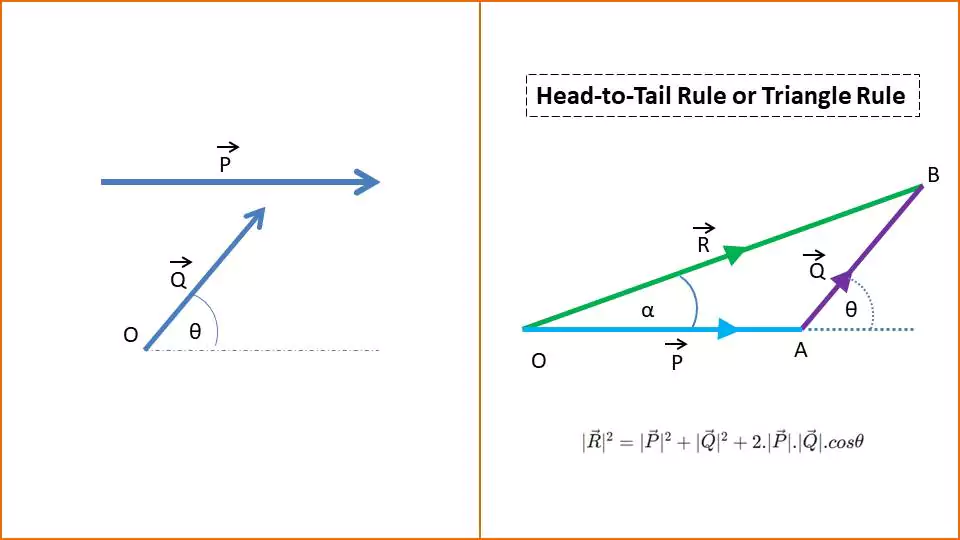
As an example, P and Q, are two vectors making an angle θ. Their resultant vector is given by OB.

Parallelogram Rule:

To find the resultant vector using parallelogram law, we need to place the vectors so they start at the same point. Now we complete a parallelogram using the vectors as adjacent sides. The diagonal of the parallelogram represents the resultant vector.

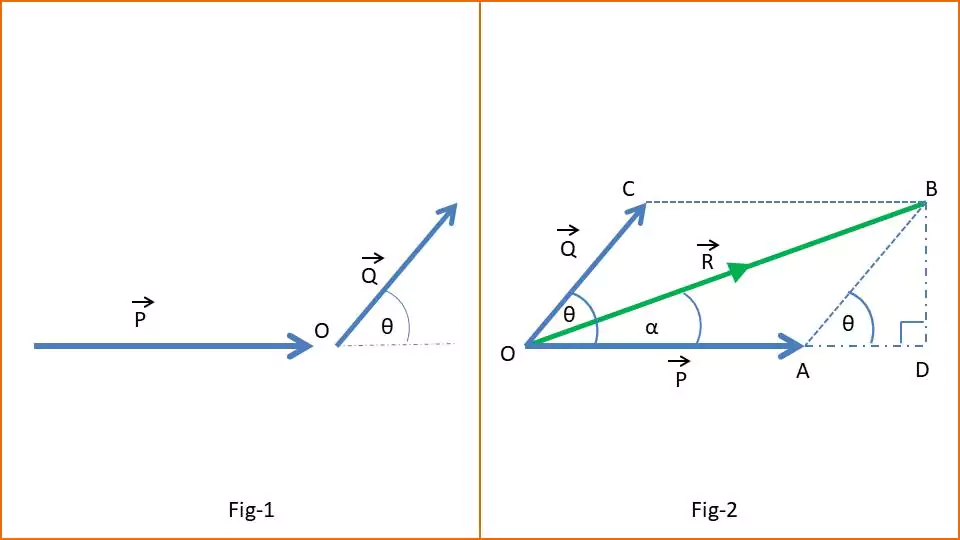
For example, vectors P and Q give the resultant vector OB.

OB²=OA²+AB²+2.OA.AB.cosθ

Algebraic Method (Component)

In this method, we need to split the vectors into their components – for 2D (x and y components) and 3D (x, y, and z components). For 2D case, let us consider the following figure.

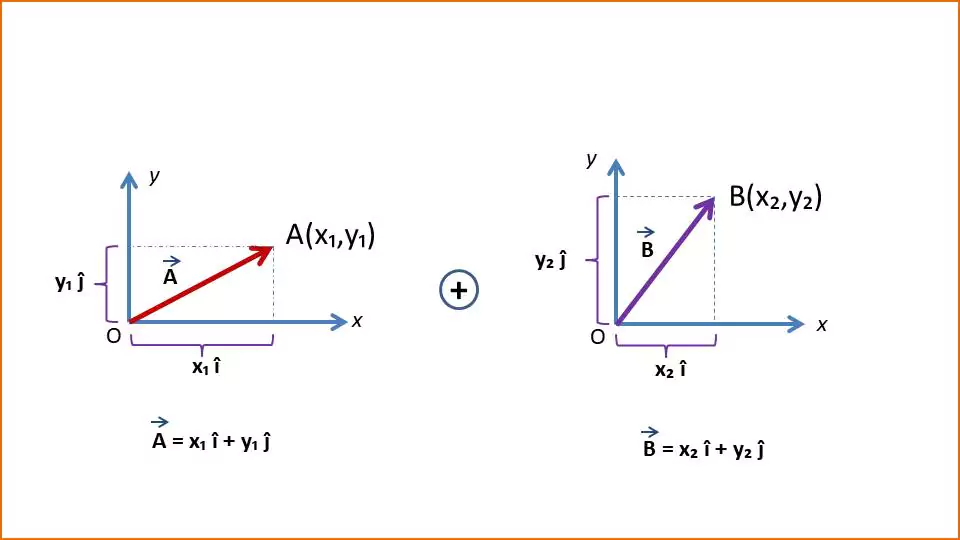
Two vectors A and B are given into their component form –

• $\vec{A} = x_1 \hat{i} + y_1 \hat{j} $
• $\vec{B} = x_2 \hat{i} + y_2 \hat{j} $

Resultant vector R after adding A and B is –

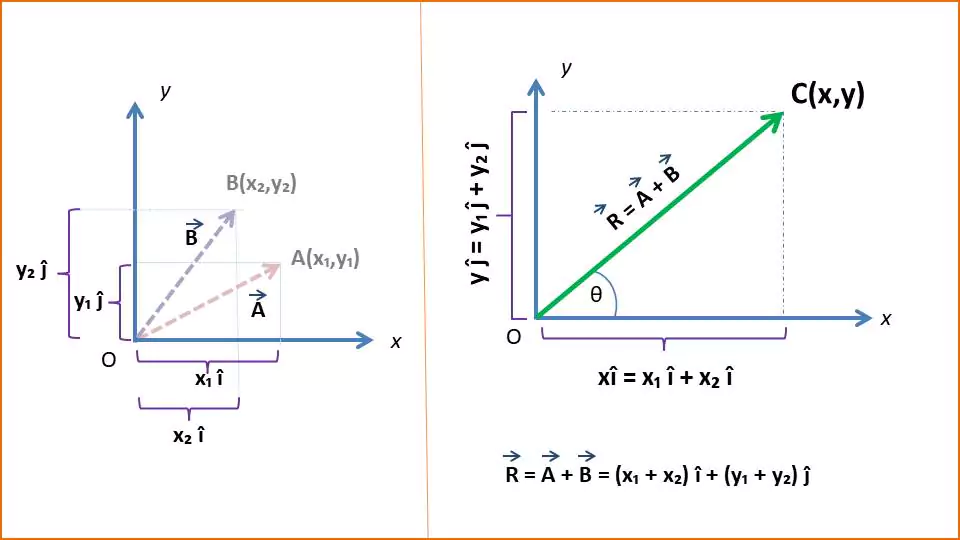
$\vec{R} = \vec{A} + \vec{B} = (x_1 + x_2)\hat{i} + (y_1 + y_2)\hat{j}$

The direction of the resultant vector is given by angle θ.

$\therefore \tan\theta= \frac{y_1+y_2}{x_1+x_2}$

In 3D, each vector have 3 components along $\hat{i}$,$\hat{j}$ and $\hat{k}$. Let’s assume 2 vectors in 3D –

• $\vec{A} = A_x \hat{i} + A_y \hat{j} + A_z \hat{k}$
• $\vec{B} = B_x \hat{i} + B_y \hat{j} + B_z \hat{k}$

The resultant vector $\vec{R}$ combines the contributions along $\hat{i}$,$\hat{j}$​, and $\hat{k}$.

$\vec{R} = \vec{A} + \vec{B} = (A_x + B_x)\hat{i} + (A_y + B_y)\hat{j} + (A_z + B_z)\hat{k}$

Examples Solutions

A person walks 3 meters east and then 4 meters north. What is their total displacement?

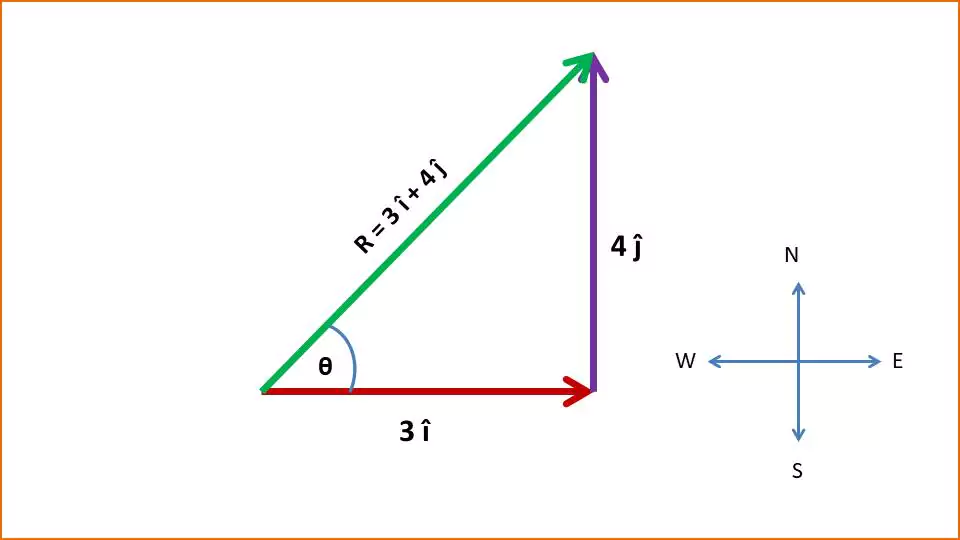
Solution: Given walking east: $\vec{A} = 3\hat{i}$ and walking north: $\vec{B} = 4\hat{j}$.

The resultant displacement $\vec{R}$ is:

$\vec{R} = \vec{A} + \vec{B} \\ \vec{R} = 3\hat{i} + 4\hat{j}$

And $R_x​=3$, $R_y = 4$

The magnitude of $\vec{R}$ is the straight-line distance:

$|\vec{R}| = \sqrt{(R_x)^2 + (R_y)^2} \\ |\vec{R}| = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5$

The direction θ (angle with the east direction, $\hat{i}$) is given by:

$\theta = \tan^{-1}\left(\frac{R_y}{R_x}\right) \\ \theta = \tan^{-1}\left(\frac{4}{3}\right) \approx 53.13^\circ$

Two forces $\vec{B} = 8\hat{i} \, \text{N}$ and $\vec{C} = 6\hat{j} \, \text{N}$ are acting on a body. What is the resultant force on the body?

Solution: The resultant force $\vec{R}$

$\vec{R} = \vec{B} + \vec{C} \\ \vec{R} = (8\hat{i}) + (6\hat{j}) \\ \vec{R} = 8\hat{i} + 6\hat{j} \, \text{N}$

So $R_x = 8$ and $R_y = 6$

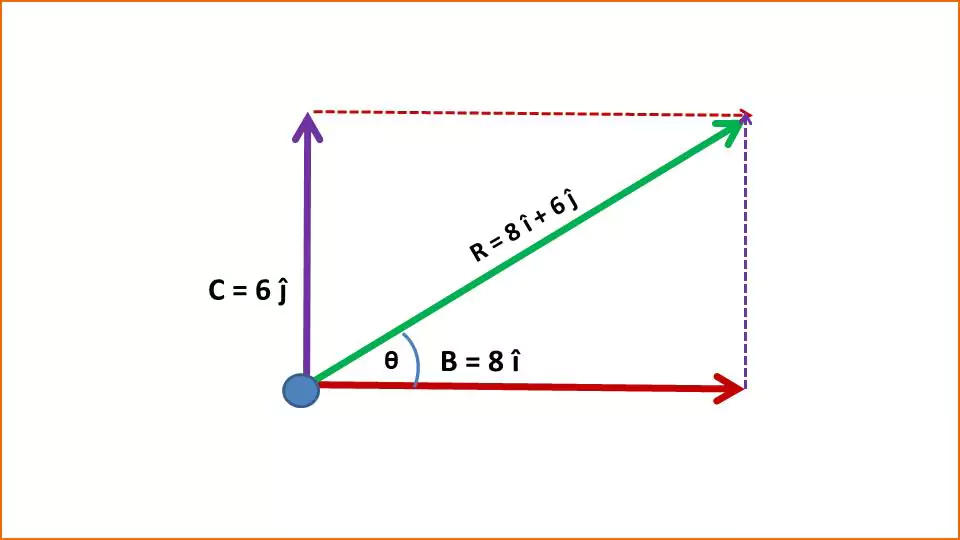
The magnitude of the resultant force $\vec{R}$ is given by:

$|\vec{R}| = \sqrt{(R_x)^2 + (R_y)^2}\\ |\vec{R}| = \sqrt{8^2 + 6^2} = \sqrt{64 + 36} = \sqrt{100} = 10 \, \text{N}$

The direction θ of the resultant force (angle with the $\hat{i}$-axis) is given by

$\theta = \tan^{-1}\left(\frac{R_y}{R_x}\right) \\ \theta = \tan^{-1}\left(\frac{6}{8}\right) = \tan^{-1}\left(0.75\right) \approx 36.87^\circ$