The law of conservation of linear momentum: If no external force acts, (that is, if all other forces except the interaction of the objects are absent), the total linear momentum of a system of bodies is always constant (in magnitude and direction).
From the above theorem, it can be said that if there are action and reaction forces between different objects in the system, the total linear momentum of the objects does not change due to this action and reaction. Only external forces can change the momentum of a system of objects. Therefore, the sum of the total momentum of the objects in a particular direction before the action and reaction remains the same after the action and reaction.
As an example, consider a head-on collision between two objects. Before the collision, an object of mass m1 is moving at a velocity u1 and another object of mass m2 is moving with a velocity u2.
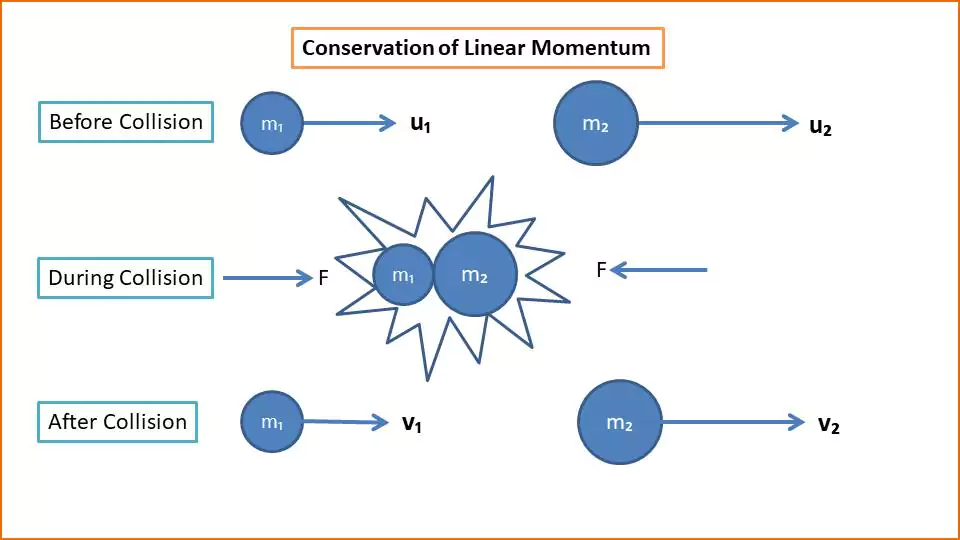
Therefore, the total momentum before the collision = m1u1 + m2u2
If the velocities of the two balls after the collision are v1 and v2,
then their total momentum = m1v1 + m2v2.
So from the conservation of linear momentum, the total momentum before the collision is the total momentum after the collision
m1u1 + m2u2 = m1v1 + m2v2
Proof from the law of motion:
During the collision of objects, two equal and opposite forces arise. Object m1 exerts a force (action) on object m2 and object m2 exerts a reaction force on object m1. From Newton’s third law-
Action by object m1 = − Reaction by object m2
F1 = − F2
Since the action and reaction act for the same time, the impulse of these two forces is equal and opposite.
Impulse of Force F1 = – Impulse of Force F2
Change in momentum of object m1 − Change in momentum of two objects m2
m1u1 − m1v1 = − (m2u2 − m2v2)
Rearranging –
m1u1 + m2u2 = m1v1 + m2v2
That is, the initial momentum of the two objects is the final momentum of the two objects.
Alternative proof:
The conservation of momentum law can also be established using calculus. Suppose the momentum of an object of mass m1 is P1 and the momentum of an object of mass m2 is P2.
From Newton’s second law
$$F_1 = \frac{dP_1}{dt}\ and\ F_2 = \frac{dP_2}{dt}$$
Now $F_{1} = − F_{2}$
$$\frac{dP_1}{dt} = − \frac{dP_2}{dt}$$
$$\therefore \frac{d}{dt}(P_1 + P_2)= 0$$
This Gives,
P1 + P2 = Constant
That is, unless an external force acts, both the magnitude and direction of the momentum of an object are constant.
Examples of the principle of conservation of linear momentum
Recoil of a gun during firing of a shell:
This is a good example in support of this principle. Before the shell is fired from the gun, the gun and the shell are stationary. That is, the total momentum of the mass is zero. When the shell is fired, it runs forward with a certain momentum. Immediately, the gun recoils with an equal and opposite momentum. Therefore, the total momentum of the mass is zero even after the shell is fired.
When a bullet is fired from a gun or cannon, the gunpowder explodes. The gas produced at high pressure pushes the bullet forward. In this case, the explosion creates a force. Then the bullet runs towards the target in front with great speed. According to the law of conservation of momentum, the bullet pushes the gun in the opposite direction with the same speed. As a result, the gun moves in the opposite direction of the bullet at a certain speed. This backward velocity of the gun is called the recoil velocity.
Based on the law of conservation of linear momentum, determine the recoil velocity of the gun:
Before firing, both the gun and the bullet were at rest; therefore, the total momentum of the hot mass is zero. After firing, suppose that the bullet of mass. is moving at a speed and the gun of mass M is moving at a speed V. So from the law of conservation of momentum-
MV + mv = 0
V = − (mv)/M
This is the recoil velocity of the gun. The negative sign in the equation means that as the bullet travels forward, the gun moves backward.
Explosion of a bomb:
The bomb explodes suddenly while passing through the air. Then it splits into several parts. These parts spread out with different velocities. If we calculate the vector sum of the momentum of the split parts at any moment, we will see that the magnitude and direction of the momentum of the bomb before the explosion are the same.
It should be remembered that the law of conservation of momentum is applicable to any type of collision, elastic, inelastic, partially elastic, etc. Newtonian mechanics is not applicable in the discussion of atoms or nuclei. But the law of conservation of momentum is applicable. Therefore, it can be said that the scope of application of the law of conservation of momentum is much wider than the scope of application of Newtonian mechanics.