Speed is a physical quantity that measures how fast an object moves from one place to another. To understand speed, let us consider an easy example. Suppose we are traveling from one place to another place by car. When we start traveling, the odometer shows 2000 km. After traveling for 4 hours we reach our destination and then the car’s odometer shows 2250 km.
During our 5 hours journey the car went to (2250 − 2000) = 250 km. Therefore in 1 hour, the car travels $\frac{250}{5}$ = 50 km. So we can understand that in 1 hour i.e. in unit time the car travels the distance is called speed. The unit time can be considered as 1 hour, 1 minute, or 1 second depending on the uses or calculations.
Here the speed is calculated as km per hour. Similarly in the S.I. unit, we calculate the speed as meters per second.
$$50\ km/h = \frac{50000\ meter}{3600\ second}$$
$$=\ 13.88\ m/s$$
Therefore the speed of the car is 13.88 m/s.
Definition:
The rate of change of distance of an object per unit time is called speed.
or
The distance traveled by an object in a unit time is called speed.
Therefore the speed is calculated as an object moves the distance divided by the time.
Formula:
If an object travels a distance x in a time t, then according to the definition
$$Speed\ (v) = \frac{Distance\ (s)}{time\ (t)}$$
$$or\ v\ = \frac{s}{t}$$
In the definition we see that the distance and time both are scalar, the speed is also a scalar quantity.
Unit and Dimension of Speed
- In SI or MKS system the unit of speed is m/s or ms−1 (meter per second)
- In CGS system the unit of speed is cm/s or cm s−1 (centimeter per second)
- In FPS system the unit of speed is foot/second.
As we know,
$$Speed\ (v) = \frac{Distance\ (s)}{time\ (t)}$$
The dimension of distance is [L] and the dimension of time is [T].
So the dimension of distance is [L]/[T] = [LT−1].
Types of Speed
Uniform Speed:
If an object covers equal distances in equal intervals of time, the speed of that object is called uniform speed. Let an object travel x distance in time t, then 2x distance is time 2t, then 3x distance in time 3t. Its speed is said to be uniform.
Non-uniform Speed:
If an object covers unequal distances in equal intervals of time, the speed of the object is called non-uniform speed. Let an object go x distance in time t, then it goes 2x distance in time t, and then it goes 1.5x distance in the same time t. Clearly, it covers unequal distances (i.e. x, 2x 1.5x) in equal intervals of time. Its speed is said to be non-uniform.
Average Speed:
In the example of the car given initially, the car did not cover an equal distance in equal time, i.e. sometimes it moved fast sometimes slow. The speed did not always remain the same. To find the speed we need to divide the total distance covered by the total time. This speed is average speed.
So the average speed is the total distance traveled divided by the total time taken.
Let a car start from point A and go to point B through points B, C, and D (as shown in Figure 1.1). The car travels a distance S1 from point A to B at a time t1, a distance S2 from point B to C at a time t2, a distance S3 from point C to D at a time t3 and at last a distance S4 from point D to E at a time t4.
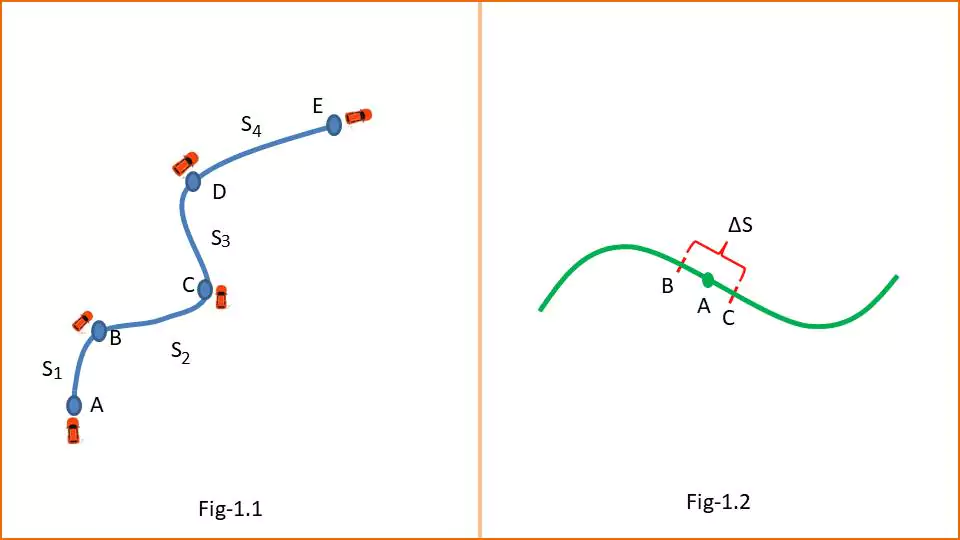
Clearly, the speed is not uniform here.
$$\text{Average Speed} = \frac{\text {Total Distance Covered}}{\text{Total Time}}$$
$$\text{Average Speed} = \frac{S_1+S_2+S_3+S_4}{t_1+t_2+t_3+t_4}$$
Instantaneous Speed
In the case of variable speed i.e. non-uniform speed, it is sometimes required to know the speed at a particular point or instant of time. In that case, the speed is called instantaneous speed.
The speed of an object at a specific instant is called instantaneous speed.
Let a particle cover a distance ΔS from point B to C (as shown in fig-1.2) at the interval of time t to (t+Δt). The average speed Va
$$V_a = \frac{\Delta S}{\Delta t}$$
If we decrease the time interval, the distance covered by the particle will also decrease. Also if the value of Δt tends to zero, the value of ΔS will tend to zero. In this situation, the limiting value of the average speed is called the instantaneous speed. Mathematically
$$v_{\text{inst}} = \lim_{\Delta t \to 0} \frac{\Delta s}{\Delta t}$$
Using Calculus,
$$v_{\text{inst}} = \left| \frac{ds}{dt} \right|$$
Speed vs Time Graph
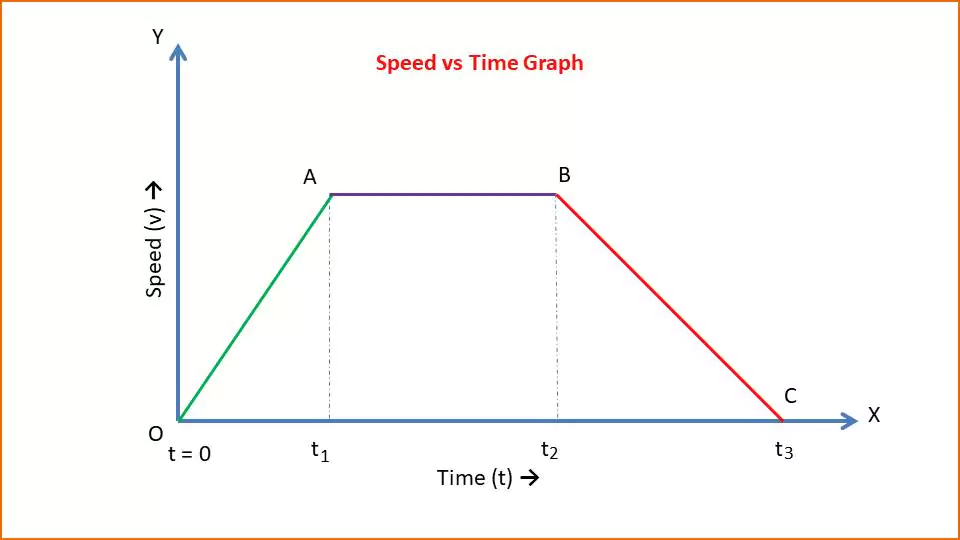
The above figure-2 shows the speed vs time graph. The X-axis and Y-axis represent the time and speed respectively.
- At time t =0, the speed of a particle is zero (Point O).
- At time t=0 to t1, its speed increases with constant acceleration (OA line).
- From time t1 to t2 its speed is constant (AB line).
- From time t2 to t3 its speed is decreasing with constant acceleration (BC line).
- At time t3 the particle comes to rest again (Point C).
Problems Solutions
A person drives a car 20 km at 40 km/h, then 30 km at 60 km/h. Find the average speed of the entire journey.
Solution: Here given S1 = 20 km and S2 = 30 km.
Step 1: First we need to calculate the time taken for each part. Let t1 be the time taken to cover 20 km at 40 km/h
$$t_1 = \frac{\text{distance}}{\text{speed}} = \frac{20}{40} = 0.5 \text{ hours}$$
If t1 be the time taken to cover 30 km at 60 km/h –
$$t_2 = \frac{30}{60} = 0.5 \text{ hours}$$
Step 2: Now we should find the total time taken by the car to cover the total distance.
Total distance covered = S1 + S2 = 20+30 = 50 km.
The total time taken to cover this 50 km is t1+t2 = 0.5 + 0.5 = 1 h.
Step 3: So the average speed Va
$$\text{Average Speed} = \frac{\text{Total Distance}}{\text{Total Time}}$$
$$V_a = \frac{S_1+S_2}{t_1+t_2}$$
$$V_a = \frac{50}{1}$$
$$=50 \text{km/h}$$
A particle moves along a straight line with its position given by: s(t)=4t2+5t+3. Find its instantaneous speed at t=3 seconds.
Solution: Given the variable position s(t)=4t2+5t+3.
We know the Instantaneous speed is given by
$$v_{\text{inst}} = \left| \frac{ds}{dt} \right|$$
First we need to differentiate s(t) w.r.t t:
$$\frac{ds}{dt} = \frac{d}{dt} (4t^2 + 5t + 3)$$
$$= 8t+5$$
Now, substituting t=3
$$v_{\text{inst}} = \left| 8(3) + 5 \right|$$
$$= 29 \text{ m/s}$$
Thus, the instantaneous speed at t=3 seconds is 33 m/s.