From Newton’s first law of motion, we know that an external unbalanced force is responsible for the change in the velocity of an object. Now, the greater this applied force, the greater the change in the velocity or acceleration of a particular object. If the applied force is doubled, the acceleration produced is doubled. In this case, the direction of the applied force and the acceleration produced are also the same. The concept of force that can be obtained from Newton’s first law of motion is naturalistic. The quantitative concept of force can be obtained from the second law of motion.
Understanding the Second Law of Newton
Suppose you are sitting in a car. The driver started the car and set it in motion. The car’s engine exerted force on the car, which made the car move. The driver increased the speed of the car to a certain value with the help of the accelerator. The accelerator creates the acceleration of the car. So it is understood that the force applied by the engine is responsible for the acceleration of the car. Now, if the force applied by the engine increases, the acceleration of the car will also increase.
So it can be seen that there is a relationship between the force applied on an object and the acceleration of the object. According to Newton’s second law of motion, the force applied on an object of a given mass is proportional to the acceleration of that object and the direction in which the applied force acts is also the direction of the acceleration produced.
To simplify the above example, we can conclude that if an object experiences no force or a balanced force, it will be at rest or move with constant velocity. If an unbalanced force exists, there will be an acceleration that is directly proportional to the applied force and inversely proportional to the object’s mass.
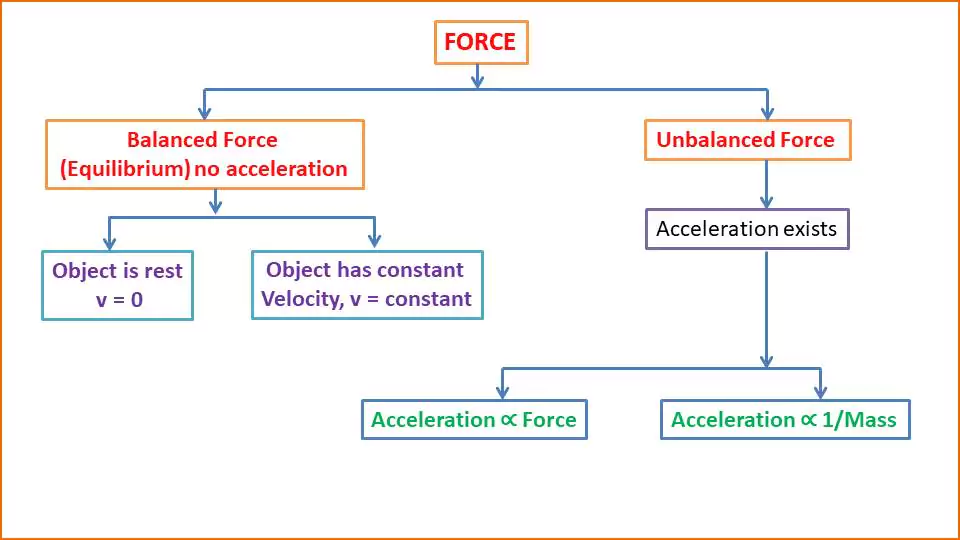
Statement of Newton’s Second Law:
The rate of change of momentum of an object is directly proportional to the force applied on the object and the change in momentum occurs in the direction in which the force is applied.
The acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. The direction of the acceleration is in the direction of the net force.
Derivation of the Equation of Force from the Newton’s Second Law
When a force is applied to an object, the velocity of the object changes. As a result, the momentum also changes. According to Newton’s second law, the rate of change of this momentum, i.e. the change in momentum per unit time, is proportional to the applied force.
Analytic Method
Let us assume that the initial velocity of an object is u with mass m. The acceleration of the object due to a force F acting on the object is ‘a‘
And the velocity after time t is v.
The initial momentum of the object is mu.
After time t,
The final momentum of the object is mv.
So the change in momentum after time t is = mv − mu
Rate of change of momentum = (mv − mu)/t = {m(v − u)}/t = ma …….. [eqn 1]
Where (v – u)/t = a = acceleration.
So from the second law, the applied force F is directly proportional to the change in momentum.
F ∝ ma
F = Kma …….. [eqn 2]
K is a constant. Its value depends on the unit of force.
If the force that acts on an object of unit mass and produces a unit acceleration in the object is considered as a ‘unit force‘, i.e. if m = 1 a = 1 gives F = 1 then K = 1. Therefore, according to this definition of the unit of force, we get K = 1. from …….. [eqn 2] we get,
F = ma
i.e. applied force (F) = mass of the object (m) × acceleration produced in the object (a).
Info: 1 Newton is defined as the force required to accelerate a 1 kg object by 1 m/s².
Using Calculus
Newton’s Second Law can be derived from the concept of momentum. Momentum ($\vec{p}$) is defined as the product of mass and velocity:
$$\vec{p} = m \vec{v}$$
According to Newton’s Second Law, the rate of change of momentum is proportional to the net force applied
$$\vec{F} \propto \frac{d\vec{p}}{dt}$$
Substituting $\vec{p} = m \vec{v}$, we get:
$$\vec{F} \propto \frac{d}{dt} (m \vec{v})$$
If the mass m is constant,
$$\vec{F} \propto m \frac{d\vec{v}}{dt}$$
Since $\frac{d\vec{v}}{dt} =a$ (acceleration), we get:
$$\vec{F} \propto m \vec{a}$$
Introducing the proportionality constant K
$$\vec{F} = K m \vec{a}$$
As discussed above if m = 1 a = 1 gives F = 1 then K = 1
$$\vec{F} = m \vec{a}$$
Info: If multiple forces act on a body, the total force is the vector sum of all individual forces: $\vec{F}_{\text{net}} = \sum \vec{F}_i$
Mathematical Expression:
Newton’s Second Law is expressed mathematically as:
$$\vec{F_{net}} = m\vec{a}$$
Where:
- $\vec{F_{net}}$ = Net force acting on the object (vector quantity, measured in Newtons, N)
- m = Mass of the object (scalar quantity, measured in kilograms, kg)
- $\vec{a}$ = Acceleration of the object (vector quantity, measured in meters per second squared, m/s²)
Info: Newton’s Second Law is valid only in inertial frames of reference (non-accelerating frames).
Newton’s First Law from the Second Law
Let the mass of an object be m. Applying force F, an acceleration a is created. From 2nd law
F = ma
F = m (v – u)/t
If applied force F is zero i.e. F = 0/
0 = m (v – u)/t
or, m (v – u) = 0
or, (v – u) = 0
v = u
So if no external force is applied to an object, the object will be at rest or will have constant velocity.
Mass is a measure of inertia-Explanation from Newton’s Second Law
We have already learned that inertia is the property of an object that prevents it from changing its state of rest or motion along a straight line.
The force required to change the state of motion of an object depends on the mass of the object. The greater the mass of the object, the greater the force required.
Suppose two objects of mass m1 and m2 are acted upon by forces of the same magnitude F. As a result, the acceleration of the first object is a1, and the acceleration of the second object is a2, then F=m1a1, and F=m2a2. Therefore, m1a1=m2a2
a1/a2 = m2/m1
or, a ∝ 1/m
That the acceleration is inversely proportional to the mass under the same applied force.
If the mass is more, the acceleration will be less, that is, the more mass of the object, the harder it is to change its velocity. The object whose velocity is hard to change has more force. Therefore, it can be said that the force depends on the mass of the object. If the mass is more, the force will be more. Therefore, it can be said that mass is the measure of the force of the object. That is, force can be measured by mass.
Problems Solutions
A body of mass 5 kg is accelerating at 2 m/s². Find the force acting on it.
Solution: We have mass m = 5 kg, acceleration a = 2 m/s²,
Force F = ma = 5 × 2 = 10 N.
A force of 30 N acts on a 4 kg mass. Find its acceleration.
Solution: Here we have force F = 30 N and mass m = 4 kg. If a is the acceleration then,
F = ma
or, a = F/m
or, a = 30/4 = 7.5 m/s²
A 5 kg particle is subjected to two forces: $\vec{F}_1 = (10\hat{i} + 5\hat{j})$ and $\vec{F}_2 = (-2\hat{i} + 3\hat{j})$ . Find the acceleration vector of the particle.
Solution: The net force acting on the particle is: Fnet = F1 + F2
$$\vec{F}_{\text{net}} = (10\hat{i} + 5\hat{j}) + (-2\hat{i} + 3\hat{j})$$
$$\vec{F}_{\text{net}} = (10 – 2)\hat{i} + (5 + 3)\hat{j} = (8\hat{i} + 8\hat{j}) \text{ N}$$
Using Newton’s Second Law
$$\vec{a} = \frac{\vec{F}_{\text{net}}}{m} = \frac{(8\hat{i} + 8\hat{j})}{5}$$
$$\vec{a} = 1.6\hat{i} + 1.6\hat{j} \text{ m/s}^2$$
A 2 kg object is dropped from a height, experiencing only gravity and a constant upward force of 10 N due to air resistance. Find its acceleration.
Solution:
Gravity force (weight)
$$F_g = m g = 2 \times 9.8 = 19.6 \text{ N} \quad (\text{downward})$$
Upward force due to air resistance
$$F_{\text{air}} = 10 \text{ N} \quad (\text{upward})$$
Net force:
$$F_{\text{net}} = F_g – F_{\text{air}} = 19.6 – 10 = 9.6 \text{ N}$$
Using Newton’s Second Law
$$a = \frac{F_{\text{net}}}{m} = \frac{9.6}{2} = 4.8 \text{ m/s}^2$$
Since the net force is downward, the object accelerates downward at 4.8 m/s².