Two types of physical quantities, scalars and vectors, are required for various mathematical calculations in physics. Some of them have no particular direction (scalars) and some of them have a proper direction (vectors). In other words, physical quantities are categorized into two types- scalar and vector based on the direction.
Scalar
Definition of Scalar: A physical quantity that has only the magnitude (numerical value or size) but not the direction, is called Scalar quantity.
Characteristics of Scalar Quantities:
- A scalar quantity is only represented by a number with its appropriate unit.
- It has no fixed direction i.e. scalars do not depend on direction.
- Scalar quantities follow simple algebra rules, like addition, subtraction, multiplication, or division.
- Scalars don’t change under the rotation of coordinates.
Example of scalar quantities:
- Mass (m = 3 kg)
- Time (t = 15 seconds)
- Length (l= 20 m)
- Volume (V = 4 m3)
- Density (ρ = 1000 kg/m3)
- Speed ( v = 10 m/s)
- Work (W = 10 J)
- Energy (E = 12 erg)
- Power (P – 746 Watt)
- Temperature (θ = 98.4° C )
- Potential (1.5 Volts)
- Specific heat (5)
- Refractive index (1.5)
- Wavelength (0.25 m)
- Electric Current (2.5 Ampere)
- Charge (7 Coulombs)
- Pressure (1.01325 × 105 N/m2)
- Frequency (50 Hz)
- Etc…
All the examples mentioned above have only the magnitude or value, not the direction.
Extra Info: Scarar is a Tensor of Rank-0.
Vectors
Definition of Vector: A physical quantity that has both the magnitude and the direction is called Vector quantity.
Another way we can say that, Physical quantities that require both magnitude and direction to be expressed and that follow the rules of vector addition are called vector quantities.
For example, if we say that the force applied on an object is 15 N, it is not complete to say about the force. It is necessary to specify in which direction the force acts, i.e. the direction of action of the force. To describe any vector quantity accurately, both its magnitude and direction have to be specified.
Characteristics of Vector Quantities:
- Magnitude and direction, are both required to fully describe a vector.
- Vectors generally do not follow the rule of simple algebra.
- The vector changes if the magnitude or direction or both change.
- Vector changes under the rotation of coordinates.
- It follows the rules of vector addition, such as the triangle or parallelogram law.
- The resultant vector produced by adding two vectors is completely dependent on the angle made by those two vectors.
- There are two types of vector product – one is scalar product (or dot product) which gives scalar and the other is vector product (or cross product) which gives another vector.
Info: We can not divide a vector by another vector. Because division by a vector does not give any precise result.
Example of Vector quantities:
- Displacement (10 m along East)
- Velocity (Linear and angular)
- Weight (9.8 N always directed towards the center of the earth)
- Force (10 N along North)
- Momentum (Linear and angular)
- Torque
- Electric Field
- Magnetic Field
- etc.
Understanding Scalar & Vector
To understand scalar and vector visually, let us consider the following figure-

Let us consider a bike starts moving from point A along the red path. It will cover the point 1, 2, 3, and 4, and finally reach the point B. In this case, it has no particular direction. So the total path cover is called distance which is a scalar quantity. Now if the bike starts moving along the green straight-line path, then it has a particular direction indicated by an arrowhead. So the green AB path is called displacement which is a vector quantity.
Note: Having the magnitude and direction is not ‘the sufficient‘ condition to be a vector quantity. Physical quantity should have to follow (necessary condition) the rules of vector addition. For example: Electric current has both the magnitude (in ampere) and direction (from one end of a straight wire to another end). However electric current is a scalar quantity (because it does not obey the rule of vector addition).
Extra Info: What about the Area? Is it a Scalar or Vector? Well, Area is often considered to be a scalar quantity. But if we associate a vector with it along the normal ( i.e. perpendicular) of this area, then the magnitude of the area and this normal vector combined give the Area Vector. This area vector is a Vector quantity. In physics, we use area as an area vector in many applications.
Extra Info: Vector is a Tensor of Rank-1.
Representation of a Vector
Geometrically a vector is represented by an arrow “→” (or a straight line pointing in a direction by an arrowhead symbol). The length of the arrow determines the magnitude and the direction of the arrow is the direction of the vector. In this case, two points (initial or starting point and final or endpoint) are connected by a straight line.
Analytically a vector is represented by placing an arrow above a symbol or one letter or two letters. Example: Angular velocity: $\overrightarrow{\omega }$, Force $\overrightarrow{F}$ or Displacement $\overrightarrow{AB}$. And |$\overrightarrow{F}$| or |$\overrightarrow{AB}$| represents their magnitude.
In a simple mathematical expression:-
Vector = Magnitude with direction.
or, Vector = Magnitude with unit vector.
or, $\vec{A}= |\vec{A}|\hat{n}$ , where $\hat{n}$ is the unit vector along $\vec{A}$ and $|\vec{A}|$ = magnitude
In algebra, a vector can be represented in a cartesian coordinate system (one, two, or three-dimensional), polar coordinate system (2-D), spherical coordinate system (3-D) etc.
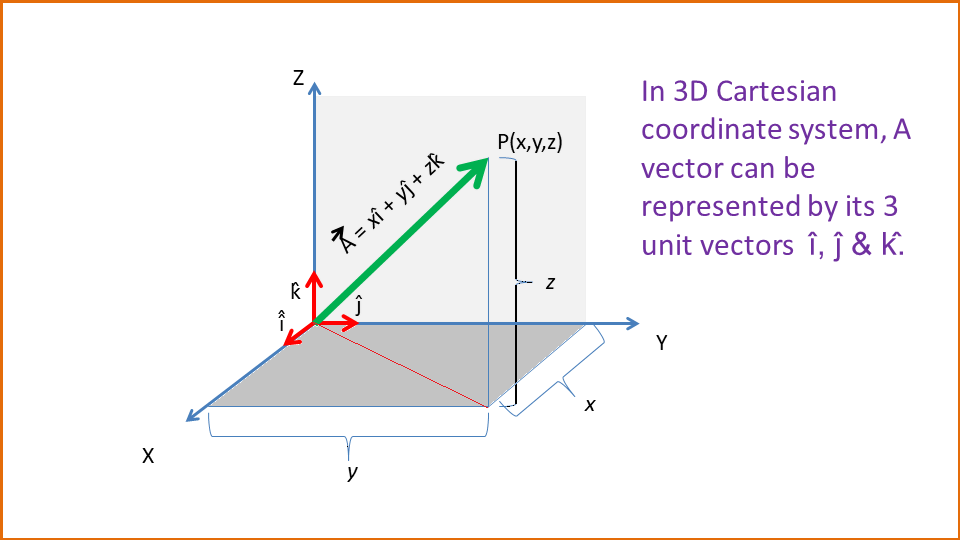
Example in 3-D Cartesian: $\vec{A} = x\hat{i}+y\hat{j}+z\hat{k} $
Example in 2-D Polar: $\vec{A} = A_{r}\hat{r}+A_{\theta }\hat{\theta}$
Example in Spherical: $\vec{A}= A_{r} \hat{r} + A_{\theta}\hat{\theta} + A_{\phi}\hat{\phi}$
Key Differences
| Property | Scalar | Vector |
|---|---|---|
| Magnitude | Only magnitude | Magnitude and direction |
| Direction | Not applicable | Always specified |
| Example | Mass, time, speed | Force, velocity, acceleration |
| Mathematical Ops | Added/subtracted directly | Added/subtracted using vector rules (triangle/parallelogram law) |