Projectile Motion

Projectile motion is a two dimensional motion with uniform acceleration. When an object is thrown or projected into the air with an angle, initially it reaches some height and then it comes back to the earth’s surface covering some horizontal distance. The acceleration due to gravity acting on the object is uniform. The object moves in a curved path called a trajectory, which is a parabola.

Projectile: An object thrown upwards at an angle to the horizontal is called a projectile.

Projectile Motion: Projectile motion is the two-dimensional motion of an object under the influence of uniform gravity. In projectile motion, the object follows a curved path which is a parabola. It occurs when an object has both an initial horizontal and vertical component of velocity along with vertical acceleration due to gravity i.e. the object has to be thrown at an angle with the earth’s surface.

Terms in Projectile Motion:

• Velocity of projection: The initial velocity with which the projectile is projected is called the velocity of projection.
• Angle of projection: The angle at which the projectile is projected with respect to the horizontal is called the angle of projection.
• Range of projection: The distance from the point of projection to the point on the vertical plane drawn through the projectile point at which the projectile returns and meets the projectile point is called the range of projection of the projectile.
• Time of Flight or Time of ascend: The time the projectile remains in the air is called the Time of Flight.

Assumption:

• The acceleration of the ball at any point in its path is downward and equal to the acceleration due to gravity (g). That is, if we project a ball, its acceleration along the vertical is $a_{y} = g$
• The projectile has no acceleration along the horizontal. That is, $a_{x} = 0$
• Air resistance will be ignored.
• Changes in gravitational acceleration will be ignored in discussing the projectile motion.
• The only force acting on the ball is its weight.

Equation of Motion of Projectile Motion

Let us consider an object is projected at an angle θ (< 𝞹/2) with the horizontal axis with initial velocity u. In the following figure, an object is projected from point O at an angle θ with the x-axis. It travels along the OPQB path and touches the ground at point B. At point A the maximum height of the projectile is H and it covers a horizontal distance which is the range of the projectile is OB =R.

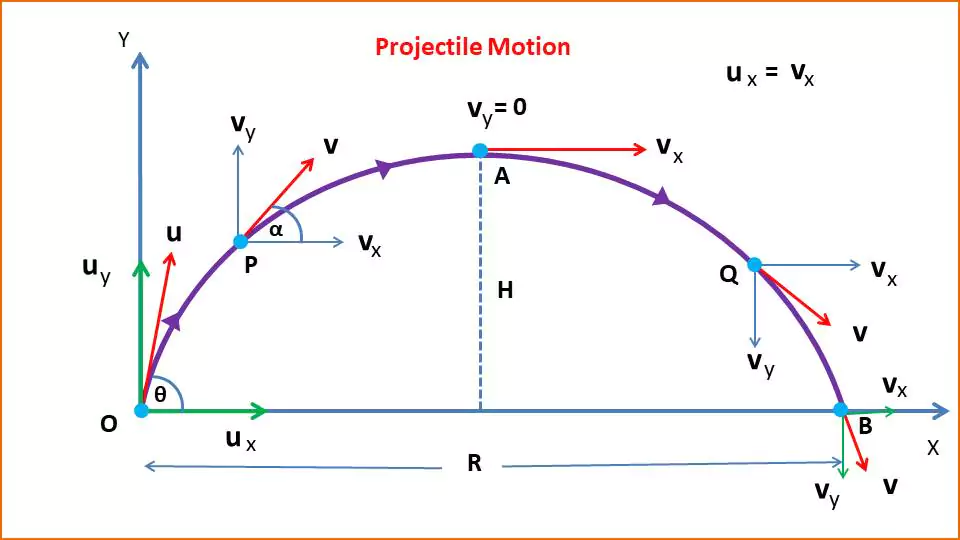
The initial velocity of the projectile at point O is u. The x and y components of u along the x and y axis respectively are –

• u_x = u cosθ
• u_y = u sinθ

The gravitational acceleration (g) has no horizontal component (g_x = 0). It has only a vertical component (g_y = g). The displacement (s) of an object after time t and velocity v is equal to velocity multiplied by time i.e

Displacement = velocity × time.

So after time t the horizontal displacement (x) of the projectile is

$$x = u_x × t$$

$$ \begin{gather} x = u\ \text{cos}\theta \cdot t \end{gather}$$

$$or\ t = \frac{x}{u\cdot \text{cos}\theta }$$

For the vertical motion we need to consider the gravitational acceleration g. The displacement (s) of an object after time t with initial velocity u and acceleration g is given by

$$s = ut + \frac{1}{2}gt^{2}$$

In this case the initial vertical velocity of the projectile is uy and acceleration is = −g.

So the vertical displacement of the projectile after time t is

$$\begin{gather} s = u\ \text{sin}\theta\cdot t – \frac{1}{2}gt^{2} \end{gather}$$

By putting the value of t from equation 1 into equation 2 we get

$$s = u\ \text{sin}\theta\cdot \frac{x}{u \text{cos}\theta } – \frac{1}{2}g\cdot \frac{x^2}{u^2 \text{cos}^2\theta}$$

$$\begin{gather} \therefore s = x\ \text{tan}\theta – \frac{gx^2}{2u^2 \text{cos}^2\theta} \end{gather}$$

The above equation is an equation of parabola –

$${\displaystyle y=ax^{2}+bx+c}$$

Therefore the equation of the path of a projectile is a parabola.

Important relation of projectile

Time to ascend maximum height (t₁):

We have initial vertical velocity u_y. After time t the vertical velocity will be

v_y = u⋅sinθ − gt

Now at the maximum height, the verticle velocity of the projectile is v_y = 0. And the time taken to reach this maximum height is t₁. Applying (v = u − at) in this case we get.

0 = u⋅sinθ − gt₁

$$ \begin{gather} \therefore t_1 =\frac{u\cdot \text {sin}\theta }{g} \end{gather}$$

Maximum height (H) of projectile

If the projectile reaches its maximum height then as discussed above its verticle component of velocity is zero i.e v_y = 0. Applying (v² = u² − 2as) formula we get –

0 = u_y² − 2gH

0 = u²⋅sin²θ − 2gH (Putting u_y = u⋅sinθ)

$$ \begin{gather} \therefore H = \frac{u^2\cdot \text{sin}^2\theta }{2g} \end{gather}$$

Total Time of Flight/Ascend (T)

The projectile starts moving at time t = 0 from height h = 0; next, it reaches max height (H) at t₁ and returns to the ground (h = 0) at time t₂. Also, the time taken to reach max height should be the time taken to return ground, i.e. t₁ = t₂. Therefore the whole time of flight is T = t₁+t₂.= 2t₁.

$$\therefore T = 2t_1 = \frac{2u\cdot \text {sin}\theta }{g}$$

Another way we can cross-check this above equation. After time of total flight its height h = 0, so applying the formula [s = ut − (1\2) at²] we get –

0 = u⋅sinθ⋅T − (1/2) gT².

$$\begin{gather} \therefore T = \frac{2u\cdot \text {sin}\theta }{g} \end{gather}$$

Range of Projection

The horizontal velocity of the projectile is ux which remains constant. The total time of flight is T. So total horizontal displacement (R) = horizontal velocity × total time of flight.

R = u_x × T

R = u⋅cosθ × T

Putting the value of $T = \frac{2u\cdot \text {sin}\theta }{g} $ and 2sinθcosθ = sin2θ

$$ R = u\cdot \text{cos}\theta \cdot \frac{2u\cdot \text{sin}\theta }{g}$$

$$\begin{gather} \therefore R = \frac{u^2\cdot \text{sin}2\theta }{g} \end{gather}$$

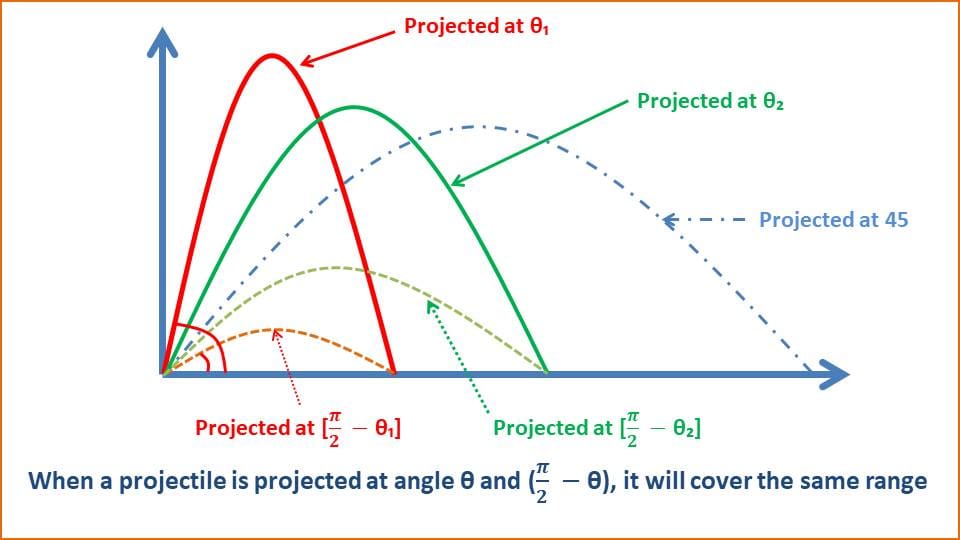
From the above equation, The maximum range R = R_max when sin2θ has maximum value i.e. sin2θ = 1.

sin2θ = 1 = 90°

or θ = 45°

Therefore, if the projectile is projected at an angle 45° with the horizontal, it will cover the maximum range (horizontally).

Now if the angle of projection is $\big ( \frac{\pi }{2} -\ \theta \big )$, than range –

$$R = \frac{u^2}{g}\cdot \text{sin}\ 2\ \bigg (\frac{\pi }{2} -\ \theta \bigg )$$

$$or\ R = \frac{u^2}{g}\cdot \text{sin} (2\pi -\ 2\theta )$$

$$or\ R = \frac{u^2}{g}\cdot \text{sin}2\theta$$

So if the angle of projection is θ and $\left ( \frac{\pi }{2} – \theta \right )$, the range will be the same.

Velocity of Projectile at any point of trajectory.

Considering figure-1, let P be a point on the trajectory of the projectile. The velocity at this point is v which makes an angle α with the horizontal axis.

As the horizontal velocity remains same –

v cosα = u cosθ

Squaring both sides we get

$$\begin{gather} v^2cos^2α = u^2cos^2θ \end{gather}$$

Its vertical velocity at this point is v sinα. Applying v² = u² − 2gh we get

$$\begin{gather} v^2 sin^2α = u^2sin^2θ − 2gh \end{gather}$$

(where u sinθ is the initial vertical velocity).

Adding the above two equations we get

v² cos²α + v² sin²α = u² cos²θ + u² sin²θ − 2gh

or, v² (cos²α + sin²α) = u² (cos²θ + sin²θ) − 2gh

[As (cos²θ + sin²θ) = 1]

$$\begin{gather} v^2 = u^2 − 2gh \end{gather}$$

This is the equation of velocity at any point on the trajectory of a projectile.

Also by dividing both those equations, we get

$$\frac{v^2 sin^2α }{v^2 cos^2α } = \frac{u^2 sin^2θ – 2gh }{u^2 cos^2θ}$$

$$tan^2 \alpha = \frac{u^2 sin^2θ – 2gh }{u^2 cos^2θ}$$

$$tan \alpha = \sqrt{\frac{u^2 sin^2θ – 2gh }{u^2 cos^2θ} }$$

$$\begin{gather} \therefore tan\ \alpha = \frac{\sqrt{ u^2 sin^2θ – 2gh }}{u cosθ} \end{gather}$$

Kinetic and Potential Energy of Projectile Motion

Kinetic energy of a projectile at the maximum height

When the projectile reaches its maximum height, its vertical velocity becomes zero. It has only the horizontal velocity at the highest point. So the horizontal velocity u_x = u cosθ contributes its kinetic energy which is minimum at this point.

$$ E_k = \frac{1}{2}mu_x^2 $$

$$\begin{gather} E_k = \frac{1}{2}m u^2 \text{cos}^2\theta \end{gather}$$

Potential energy of a projectile at the maximum height

Clearly at maximum height its potential energy will be maximum.

$$E_p = m g \cdot H $$

Putting the value of H ($= \frac{u^2 \text{sin}^2\theta }{2g}$)

$$E_p = mg \times \frac{u^2 \text{sin}^2\theta }{2g}$$

$$\begin{gather} \therefore E_p = \frac{1}{2}mu^2 \text{sin}^2\theta \end{gather}$$

Total energy = kinetic energy + potential energy.

$$\text {total energy,}\ E_k = E_k + E_p$$

$$E = \frac{1}{2}m u^2 \text{cos}^2\theta + \frac{1}{2}mu^2 \text{sin}^2\theta$$

$$E = \frac{1}{2}m u^2 (\text{cos}^2\theta + \text{sin}^2\theta)$$

$$\begin{gather} E = \frac{1}{2}m u^2 \end{gather}$$

Clearly this is the equation of initial total energy. Therefore we can say that in projectile motion the total energy of the projectile is conserved.

Body projected horizontally from a certain height

Let us consider a projectile is projected horizontally with initial velocity V₀ (along OX) (See figure-3 below). The trajectory of the projectile is OPB. After the projection there are two types of motion are involved.

1. Horizontal motion with constant velocity
2. Vertical motion with constant gravitational acceleration.

For these two types of motions, the projectile displaced along OX and OY. The x component of initial velocity is V_ox = V₀ and y component of initial velocity is V_0y = 0.

Therefore the horizontal displacement along X axis after time t is

x = V_0x × t = V₀ × t —- (a)

t= x/V₀

And the vertical displacement after time t is

y = V_0yt − (1/2)gt².

y = − (1/2)gt² —- (b)

Putting the value of t= x/V₀ from (a) into (b)

$$y= -\frac{1}{2}g\cdot \left ( \frac{x}{V_0} \right )^2$$

$$\begin{gather} y= \frac{-g}{2V_0^2}\cdot x^2 = kx^2 \end{gather}$$

Where $k = \frac{-g}{2V_0^2}$ = Constant

The equation y = kx² is an equation of parabola. Therefore when an object is projected from a certain height its motion is also parabolic.

Velocity of the projectile:

We have the initial velocity at O along OX is V_0x = V₀ and vertical velocity V_0y = 0.

After any time t, the projectile reaches point P. At this point, its horizontal velocity is V_x = V₀ but its vertical velocity is V_y = gt.

$\therefore$ the resultant velocity at P is

$$V = \sqrt{V_x^2+V_y^2}$$

$$V = \sqrt{V_0^2+g^2t^2}$$

And if the angle of the velocity at P with the vertical is β, then-

$$\text {tan}\beta = \frac{V_0}{gt}$$

$$\therefore \beta = tan^{-1}\left ( \frac{V_0}{gt} \right )$$

Time taken to reach the ground

If the height of the projectile OY = h and it takes T1 time to reach the ground then applying s = ut + (1/2)at², we get –

H = 0 × T₁ + (1/2)gT₁²

$$\therefore T_1 = \sqrt{\frac{2H}{g}}$$

Range of the Projectile

Now if the projectile covers R distant from the point Y horizontally then its range

R = V₀ × T₁

$$\therefore R = V_0 \sqrt{\frac{2H}{g}}$$

Problem Solution