Parallelogram Law of Vectors Addition

Statements of Parallelogram law:

Law: If two similar vectors can be represented by two adjacent sides of a parallelogram in magnitude and direction, then the diagonal of that parallelogram will represent the resultant vector in magnitude and direction from the same initial point from where two vectors are drawn.

Derivation of Parallelogram Law

Geometrical Method

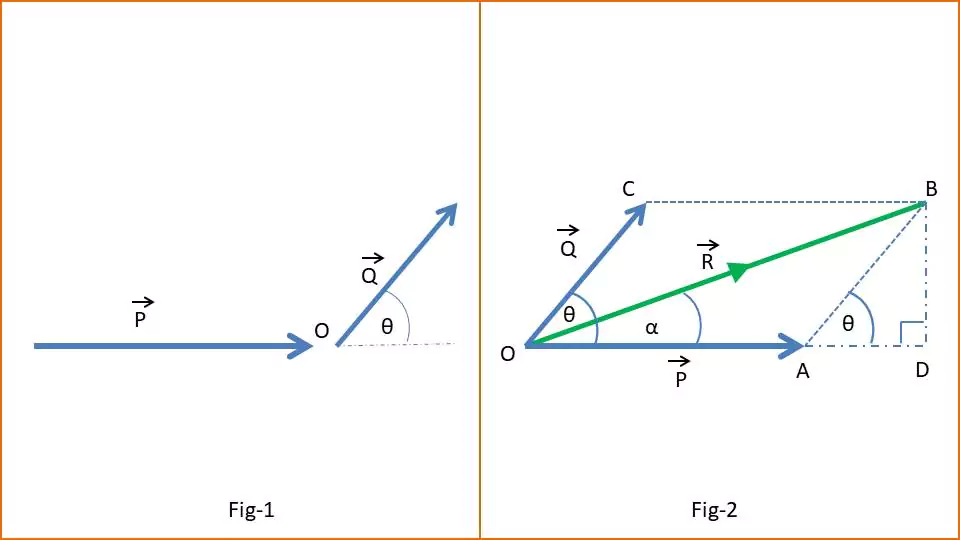
From the figure given below, let us consider two same types of vectors P and Q making an angle θ. We need to add these two vectors by parallelogram law. P and Q have the same initial point O and are represented by straight lines OA and OC respectively. Now we draw the parallelogram by connecting points A to B and C to B. Then the diagonal OB = R of this parallelogram OABC will represent the resultant vector in magnitude and direction of these two vectors P and Q.

$$\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OB} \\ \vec{P}+\vec{Q}=\vec{R}$$

Analytical Method

The magnitude and direction of the resultant vector R by adding two vectors P and Q can be calculated using geometry and trigonometry.

Finding the magnitude of Resultant Vector $|\vec{R}|$

We shall add two vectors P and Q as given in fig-1. For that P and Q are drawn from the same initial point O. OA represents the P and OC represents the Q vector. We have completed the parallelogram OABC by connecting points A to B and B to C. We also have drawn BD perpendicular to the extended line OD. So triangle ODB is a right-angle triangle; $\angle ODB = 90^{\circ}$.

$|\vec{P}| = OA\ and\ |\vec{Q}|=OC = AB$

From right angle triangle $\Delta ODB$ we get

$OB^{2}=OD^{2}+BD^{2} \\ = (OA+AD)^{2} + BD^{2} \\ =OA^{2}+AD^{2}+ 2.OA.AD+ BD^{2} \\ = OA^{2}+ 2.OA.AD+(AD^{2} + BD^{2} )\\ =OA^{2}+ 2.OA.AD+AB^{2}\\ \ =OA^{2}+ AB^{2} + 2.OA.AD$

Now from triangle $\Delta ADB$

$cosθ = \frac{AD}{AB} \\ or,\ AD = AB. cos θ$

Substituting this into above equation –

$OB^{2}=OA^{2}+ AB^{2} + 2.OA.AB. cos θ$

$|\vec{R}|^{2}=|\vec{P}|^{2}+ |\vec{Q}|^{2} + 2.|\vec{P}|.|\vec{Q}|. cos θ$

$$\fcolorbox{red}{fff} {$ \therefore |\vec{R}|=\sqrt{|\vec{P}|^{2}+ |\vec{Q}|^{2} + 2.|\vec{P}|.|\vec{Q}|. cos θ } $}$$

This equation gives us the magnitude of the resultant vector

Finding the direction of Resultant Vector $\vec{R}$

Let us consider the resultant vector $\vec{R}$ make an angle α with the vector $\vec{P}$.

From right angle triangle $\Delta ODB$ we get

$\tan\ \alpha = \frac{BD}{OD} = \frac{BD}{OA+AD} $

Putting the values of OD, BD and AD

$$\fcolorbox{red}{fff} {$\therefore \tan\alpha = \frac{Q\sin\theta}{P + Q\cos\theta}$}$$

Component Method:

Two vectors $\vec{P}$ and $\vec{Q}$​ originate from a common point O (see the fig given below). The angle between these two vectors is $\theta$. And $\vec{R}$ is the resultant vector (diagonal of the parallelogram formed by $\vec{P}$ and $\vec{Q}$​).

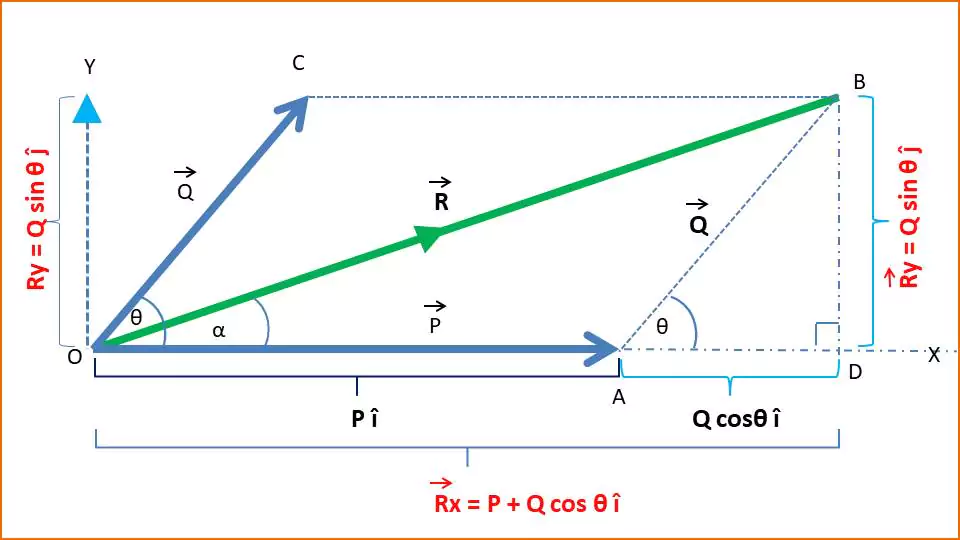
The vector $\vec{P}$ is along the x-axis: its x-component is $\vec{P} \hat{i}$ and its y-component is zero.

$\vec{P} = P_x\hat{i} \quad \text{(along x axis)}$

The x-component: $Q_x = Q\cos\theta$. and y-component: $Q_y = Q\sin\theta$.

$\vec{Q} = Q_x \hat{i} + Q_y \hat{j} $

$\vec{Q} = (Q\cos\theta)\hat{i} + (Q\sin\theta)\hat{j} $

The resultant vector $\vec{R}$ is given by:

$\vec{R} = \vec{P} + \vec{Q}\\= P\hat{i} + [Q\cos\theta)\hat{i} + (Q\sin\theta)\hat{j}]$

$\vec{R} = (P + Q\cos\theta)\hat{i} + (Q\sin\theta)\hat{j}$

This is the resultant vector it has two components

$\vec{R}$ also can be written in x and y component form.

$\vec{R} = R_{x}\hat{i}+R_{y}\hat{j}$

• $\vec{R_{x}} = (P+Q \cos \theta ) \hat{i}$
• $\vec{R_{y}} = (Q\sin\theta)\hat{j}$

Magnitude of the resultant vector is

$|\vec{R}| = \sqrt{(R_x)^2 + (R_y)^2}$

$|\vec{R}| = \sqrt{(P + Q\cos\theta)^2 + (Q\sin\theta)^2}$

$|\vec{R}| = \sqrt{P^2 + 2PQ\cos\theta + Q^2\cos^2\theta + Q^2\sin^2\theta}$

Using the trigonometric identity $\cos^2\theta + \sin^2\theta = 1$:

$|\vec{R}| = \sqrt{P^2 + 2PQ\cos\theta + Q^2}$

$\therefore |\vec{R}| = \sqrt{P^2 + Q^2 + 2PQ\cos\theta}$

The direction of $\vec{R}$ relative to $\vec{P}$ is given by the angle α.

$\tan\alpha = \frac{R_y}{R_x}$

$\tan\alpha = \frac{Q\sin\theta}{P + Q\cos\theta}$

Special Cases

Case 1: Angle $\theta = 0^\circ$ (Vectors are collinear and in the same direction)

When two vectors $\vec{P}$ and $\vec{Q}$​ are in the same direction, the angle between them is $0^\circ$. The resultant vector $\vec{R}$ will have its magnitude equal to the sum of the magnitudes of the two vectors.

Substitute $\cos 0^\circ = 1$

$|\vec{R}| = \sqrt{|\vec{P}|^2 + |\vec{Q}|^2 + 2|\vec{P}||\vec{Q}|(1)}$

$|\vec{R}| = \sqrt{(|\vec{P}| + |\vec{Q}|)^2}$

$|\vec{R}| = |\vec{P}| + |\vec{Q}|$

The direction of $\vec{R}$ is the same as that of $\vec{P}$ and $\vec{Q}$.

Case 2: Angle $\theta = 90^\circ$ (Vectors are perpendicular)

When two vectors $\vec{P}$ and $\vec{Q}$​ are perpendicular to each other, the angle between them is $90^\circ$. The resultant vector forms the hypotenuse of the right-angled triangle formed by $\vec{P}$ and $\vec{Q}$​.

$||\vec{R}|| = \sqrt{|\vec{P}|^2 + |\vec{Q}|^2 + 2|\vec{P}||\vec{Q}|(0)}$

$|\vec{R}| = \sqrt{|\vec{P}|^2 + |\vec{Q}|^2}$

The direction of $\vec{R}$ can be calculated using the tangent formula:

$\tan\alpha = \frac{|\vec{Q}|}{|\vec{P}|}$

Case 3: Angle $\theta = 180^\circ$ (Vectors are collinear but in opposite directions)

When two vectors $\vec{P}$ and $\vec{Q}$​ are in opposite directions, the angle between them is $180^\circ$. The resultant vector $\vec{R}$ will have its magnitude equal to the difference between the magnitudes of the two vectors.

Substitute $\cos 180^\circ = -1$:

$|\vec{R}| = \sqrt{|\vec{P}|^2 + |\vec{Q}|^2 + 2|\vec{P}||\vec{Q}|(-1)}$

$|\vec{R}| = \sqrt{(|\vec{P}| – |\vec{Q}|)^2}$

$|\vec{R}| = |(|\vec{P}| – |\vec{Q}|)|$

The resultant $\vec{R}$ points in the direction of the vector with the larger magnitude.

Solved Problems