Impulse of Force and Impulsive Force

The quantity, Impulse of Force, can be used to measure the effect of a force acting on an object over a certain period of time.

Definition: When a force of a constant magnitude acts on an object for some time, the product of the magnitude of that force and the time of action of the force is called the impulse of a force.

Info: Impulse is the effect of a force acting over a short period of time.

Unit of Impulse

• SI or MKS unit of impulse of force is Newton⋅second (N⋅s) or kg⋅m/s
• CGS unit of impulse of force is Dyne⋅second (dyne⋅s) or g⋅cm/s

Dimension of Impulse

We know that impulse is: J = F⋅t

Since the dimensional formula of Force (F) is: [MLT⁻²]

And the dimensional formula of Time (t) is: [T]

Multiplying these:

J = [MLT⁻²] × [T]

Dimension of Impulse is: J = [MLT⁻¹]

Mathematical Expression of Impulse

J=F⋅t

Where

• J = impulse of force
• F = force
• t = time

For a constant force:

Impulse of Force (J)= magnitude of the force (F) × time of action of the force (t)

That is, J = Ft

Now if the mass of an object is m and acceleration a, then from Newton’s second law F = ma.

So J = mat

or, J = [m (v −u)/t] × t

or, J = mv − mu …..[eqn-(1)]

J = Final momentum (mv) – Initial momentum (mu)

J = Change of Momentum (ΔP)

∴ J = ΔP

Using Calculus

The above eqn-1 can be proved using calculus. According to Newton’s second law

F = ma = m (dv/dt)

or, F⋅dt = m⋅dv

At time t = 0, initial velocity = u and at time t, final velocity = v.

Integrating both sides we get,

$$\int_{0}^{t}F\cdot dt = m\int_{u}^{v}dv$$

$$F\int_{0}^{t} dt = m(v − u)$$

… [eqn-2]

Equation (1) shows that to change the momentum of an object, a force must be applied to the object. Again, to change the momentum by the same amount, a strong force will take less time, and a weak force will take longer.

Force vs Time Graph (F-t Graph):

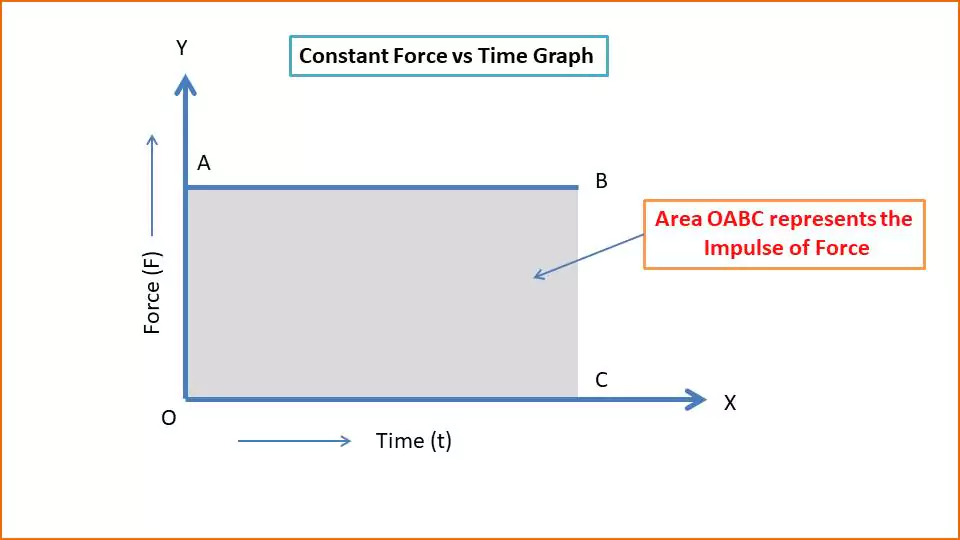
The force and time are taken along the X and Y axes respectively. The parallel line AB to the time axis represents the constant force. The area covered by the line AB with the time axis represents the Impulse of Force.

Info: If the force is constant, the graph is a rectangle, and impulse is simply F⋅t.

For a Variable Force

In most practical cases, the applied force is variable. For example, when a ball is hit with a bat or a ball is kicked with a foot, the force is variable. Usually, the force first increases and then decreases.

To find the magnitude of a force acting on a variable force acting over time. Time is divided into a number of small time intervals Δt₁, Δt₂, Δt₃ ….. Δt_n. In each small time interval, the force is assumed to be constant and the values ​​of the forces are F₁, F₂, F₃ …..F_n respectively. So the total impulse of force is

J = F₁Δt₁ + F₂Δt₂ + F₃Δt₃ + ….. +F_nΔt_n

$$J = \sum_{1}^{n} F_n\Delta t_n$$

Now if the intervals are very small such that Δt → 0,

$$J = F\int_{0}^{t} dt$$

Now F is variable, so, F = dp/dt

$$J = F\int_{0}^{t} dt = \int_{0}^{t} \frac{dp}{dt}dt$$

$$J = \int_{p_1}^{p_2} dp = P_2 − P_1 = mv − mu$$

Variable Force vs Time graph

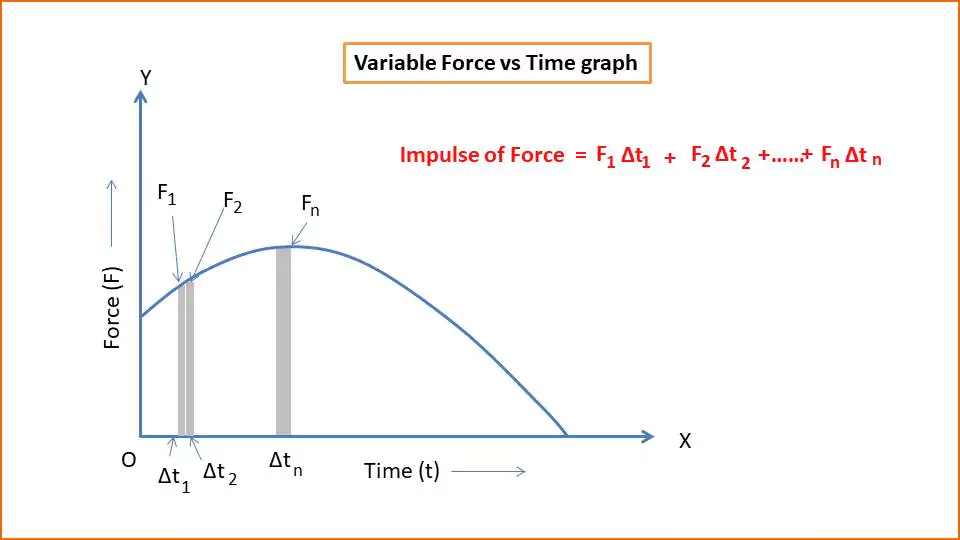
The variable force and time are taken along the X and Y axes respectively. The curve line represents the variable force. The area covered by the line with the time axis represents the Impulse of Force.

The time can be divided into a large number of small intervals Δt. For this case, we may assume the force is constant at each interval. So impulse of force due to interval Δt₁ is F₁Δt₁.

So the total impulse is J = ∑F_nΔt_n

If the Δt → 0,

$$J = F\int_{0}^{t} dt$$

Info: If the force varies, we calculate the area under the curve using integration.

Derivation of Impulse from Newton’s Second Law

Newton’s Second Law states that:

$$F = \frac{dp}{dt}$$

$$dp = F dt$$

Integrating both sides from t_i to t_f​,

$$\int_{p_i}^{p_f} dp = \int_{t_i}^{t_f} F dt$$

$$p_f − p_i = \int_{t_i}^{t_f} F dt$$

$$J = \int_{t_i}^{t_f} F dt$$

If the force is constant,

$$J = F \cdot (t_f − t_i) = F t$$

Impulsive force

When a large force acts on an object for a short period of time, such a force is called an impulsive force. For example, hitting a nail with a hammer, etc.

An impulsive force is actually a force that acts for a short period of time. Therefore, it can be said that there is no movement of the object during the action of the force. After the action of the force ends, the object starts moving and the momentum changes.

Definition: A large force acting for a very short period of time is called an impulsive force.

No noticeable movement of the object occurs during the action of the force. But in the action of this force, a measurable change in the momentum of the object occurs.

Some examples of impulsive force:

(i) When a cricket player hits the ball with a bat, the impact time is very short. Therefore, the force applied to the bat is an impulsive force.

(ii) When a nail is hit with a hammer, the force acting on the nail is large, but momentary. Therefore, an impulse force acts on the nail.

Differences between impulse of a force and impulsive force:

(i) The impulse of a force is the product of the force and the time of action of the force, but the impulse force is a large momentary force.

(ii) The impulse force creates an impact and if this force is greater, the impact of the force also increases. Therefore, it can be said that the impulsive force is the cause and the impulse of the force is its effect.

(iii) The impulsive force is a force, so its unit and the unit of force are the same. On the other hand, the unit of the impulse of the force is the same as the unit of momentum.

(iv) The momentum of the object changes due to the impulse of the force. But the effect of the impulsive force causes a large acceleration in the object in a short time.

Problems Solutions