Vectors are those which have both magnitude and direction. As vector quantities have a specific direction, their product gives us two types of result – one result has no direction i.e. scalar quantity and the other result gives a specific direction i.e. vector quantity.
The product of two vectors which gives us a scalar is called scalar product. The scalar product is represented by a ‘dot‘ (“⋅“) between two vectors – for that it is also called the dot product. So, the dot product or scalar product of two vectors $\vec{A}$ and $\vec{B}$ is denoted by $\vec{A}\cdot \vec{B}$.
Definition: The dot product is a mathematical operation (a type of multiplication) that takes two vectors and returns a scalar quantity.
Significance of Dot Product
The physical significance of dot product is “how much a vector projects onto another“. In other words it is not a product of two vectors directly (I mean not the direct product of their magnitude) rather it is a product of the component of one vector (A) along the other vector (B) with that other vector (B). The product is dependent on the angle between two vectors. Let us understand this fact with a simple example.
Consider two vectors $\vec{A}$ and $\vec{B}$ making an angle θ. Here $\vec{A}\cdot \vec{B}$ means the product of the component of A long B with the magnitude of B (fig-1). In other words the product of the projection of A onto B with B.
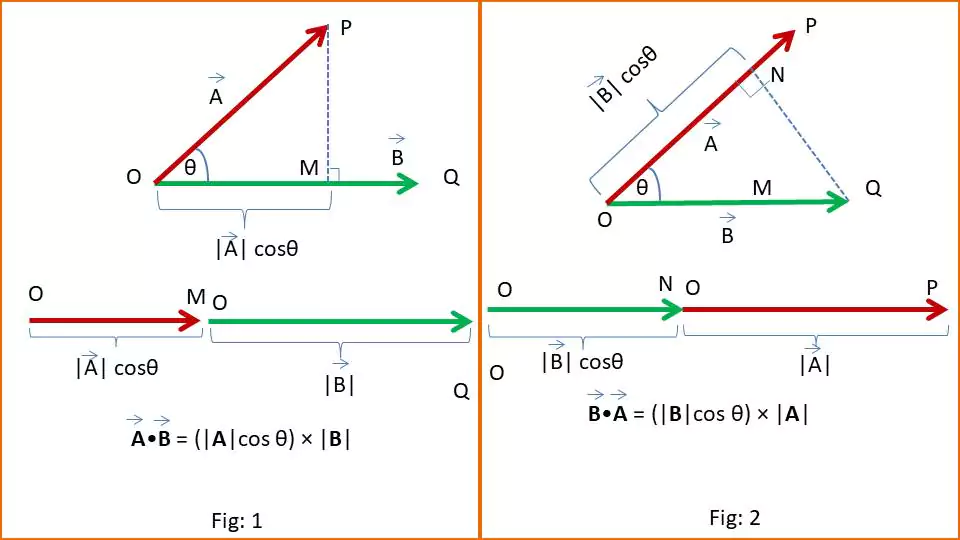
The component of $\vec{A}$ along $\vec{B}$ is equal to the projection of $\vec{A}$ onto $\vec{B}$ = $|\vec{OM}| = |\vec{A}| cos θ$. (from fig-1). So
$$\vec{A}\cdot \vec{B} = |OM| × |OQ|$$
$$= (|\vec{A}| cos θ)×|\vec{B}|$$
$$= |\vec{A}||\vec{B}|cos θ $$
$$\begin{gather} \fcolorbox{red}{#eef3f6}{$\therefore \vec{A}\cdot \vec{B} = |\vec{A}||\vec{B}|cos θ $} \end{gather}$$
Similarly, the component of $\vec{B}$ along $\vec{A}$ is equal to the projection of $\vec{B}$ onto $\vec{A}$ = $|\vec{ON}| = |\vec{B}| cos θ$. (from fig-2). So
$$ \vec{B}\cdot \vec{A} = |ON| × |OP|$$
$$= (|\vec{B}| cos θ)×|\vec{A}|$$
$$= |\vec{B}||\vec{A}|cos θ $$
$$\begin{gather} \therefore \vec{B}\cdot \vec{A} = |\vec{B}||\vec{A}|cos θ \end{gather}$$
From the above two equations (equation-1 and 2) we get –
$$\fcolorbox{red}{#eef3f6}{$\vec{A}\cdot \vec{B} = \vec{B}\cdot \vec{A}$}$$
Now if the angle θ between two vectors increases (0° to 90°), the magnitude of the projection of A onto B decreases (1 to 0). If θ further increases from 90° to 180°, the magnitude of the projection of A onto B increases in the negative direction (0 to −1).
Therefore if θ = 0°, cos0 = 1
$$\vec{A}\cdot \vec{B} = \vec{B}\cdot \vec{A} = |\vec{B}||\vec{A}|cos 0° = |\vec{A}||\vec{B}|$$
For θ = 90°
$$\vec{A}\cdot \vec{B} = \vec{B}\cdot \vec{A} = |\vec{A}||\vec{B}|cos 90°$$
$$ = |\vec{A}||\vec{B}|×0 = 0$$
For θ = 180°
$$\vec{A}\cdot \vec{B} = \vec{B}\cdot \vec{A} = |\vec{A}||\vec{B}|cos 180°$$
$$= |\vec{A}||\vec{B}|×(−1) = −|\vec{A}||\vec{B}|$$
Again the projection of $\vec{A}$ onto $\vec{B}$ is = $|\vec{OM}| = |\vec{A}| cos θ$
$$|\vec{OM}| = |\vec{A}| cos θ = |\vec{A}| (1)cosθ$$
$$ = |\vec{A}| × |\hat{b}| × cos θ = \vec{A}\cdot \hat{b} $$
$$\begin{gather} |\vec{OM}| = \vec{A}\cdot \hat{b} \end{gather}$$
where $\hat{b}$ = unit vector of $\vec{B}$, $\hat{b} = \frac{\vec{B}}{|\vec{B}|}$
$$\fcolorbox{red}{#eef3f6}{$\therefore \text{The projection of}\ \vec{A}\ onto\ \vec{B} = \frac{\vec{A} \cdot \vec{B}}{|\vec{B}|}$}$$
From the above equation (eqn-3), we conclude that if a vector is multiplied (dot product) by the unit vector of another vector, we get the projection of the first vector onto the second vector.
The projection vector $\overrightarrow{OM} = (\vec{A} \cdot \hat{b}) \hat{b}$ = $(\vec{A}\cdot \frac{\vec{B}}{|\vec{B}|})\hat{b}$
$$\begin{gather} \fcolorbox{red}{#fff}{$\therefore \overrightarrow{OM} = \bigg( \frac{ \vec{A}\cdot \vec{B}}{|\vec{B}|} \bigg) \hat{b}$} \end{gather}$$
Properties of Dot Product or Scalar Product
$\fcolorbox{orange}{#fff}{$\textbf{1}$}$ Commutative Property: If $\vec{A}$ and $\vec{B}$ are two non-zero vectors,-
$$\vec{A}\cdot \vec{B} = \vec{B}\cdot \vec{A}$$
$\fcolorbox{orange}{#fff}{$\mathbf{2}$}$ Distributive Property: $\vec{A} \neq 0$, $\vec{B} \neq 0$, and $\vec{C} \neq 0$, then
$$\vec{A}\cdot \left ( \vec{B} + \vec{C}\right ) = \vec{A}\cdot \vec{B}+\vec{A}\cdot \vec{C}$$
$\fcolorbox{orange}{#fff}{$\mathbf{3}$}$ Scalar Multiplication: When $k$ is scalar and $k \neq 0$,
$$k\left ( \vec{A} \cdot \vec{B}\right )=\vec{A}\cdot \left ( k\vec{B} \right )=\left ( k\vec{A} \right )\cdot \vec{B}$$
$\fcolorbox{orange}{#fff}{$\mathbf{4}$}$ Orthogonality: If the dot product of $ \vec{A}$ and $ \vec{B}$ is zero, i.e.
$$ \vec{A}\cdot \vec{B}=0$$
which means they are perpendicular, and we can say that $ \vec{A}$ and $ \vec{B}$ are orthogonal.
$\fcolorbox{orange}{#fff}{$\mathbf{5}$}$ Non-Negative Self-Dot Product (Magnitude)
$$\vec{A}\cdot \vec{A}=\left | \vec{A}\right |^{2}$$
$$or \left | \vec{A}\right |= \sqrt{\vec{A}\cdot \vec{A}}$$
$\fcolorbox{orange}{#fff}{$\mathbf{6}$}$ Relation to Angle Between Vectors
$$\vec{A}\cdot \vec{B}= \left | \vec{A}\right |\left | \vec{B}\right |cos\theta$$
- Parallel vectors (θ = 0°) $\vec{A}\cdot \vec{B}= \left | \vec{A}\right |\left | \vec{B}\right |$
- Anti-parallel vectors (θ = 180°) $\vec{A}\cdot \vec{B}= -\left | \vec{A}\right |\left | \vec{B}\right |$
$\fcolorbox{orange}{#fff}{$\mathbf{7}$}$ The dot product of the zero vector with any vector is zero.
$$\vec{0}\cdot \vec{B}= 0$$
$\fcolorbox{orange}{#fff}{$\mathbf{8}$}$ If $\hat{i}$, $\hat{j}$ and $\hat{k}$ are three unit vectors along X, Y and Z axis respectively in a cartesian coordinate system, then –
- $\hat{i}\cdot \hat{i}= 1$
- $\hat{j}\cdot \hat{j}= 1$
- $\hat{k}\cdot \hat{k}= 1$
- $\hat{i}\cdot \hat{j}= 0$
- $\hat{j}\cdot \hat{k}= 0$
- $\hat{k}\cdot \hat{i}= 0$
$\fcolorbox{orange}{#fff}{$\mathbf{9}$}$ If $\vec{A}=A_{x}\hat{i}+A_{y}\hat{j}+A_{z}\hat{k} \\ and\ \vec{B}= B_{x}\hat{i}+B_{y}\hat{j}+B_{z}\hat{k}$
then
- $\vec{A}\cdot \vec{B}= A_{x}B_{x}+A_{y}B_{y} + A_{z}B_{z}$
- $\vec{A}\cdot \vec{A}= A_{x}^{2}+A_{y}^{2} + A_{z}^{2}$
- $\vec{B}\cdot \vec{B}= B_{x}^{2}+B_{y}^{2} + B_{z}^{2}$
Examples of Scalar Products:
Calculate the dot product of $\vec{A} = 2\hat{i} + 3\hat{j} – \hat{k}$ and $\vec{B} = 4\hat{i} – 2\hat{j} + 5\hat{k}$
Solution: The dot product of $\vec{A}$ and $\vec{B}$ is
$\vec{A} \cdot \vec{B} = (2)(4) + (3)(-2) + (-1)(5)$
$\vec{A} \cdot \vec{B} = 8 – 6 – 5 = -3$
Find the angle between two vectors $\vec{A} = \hat{i} + 2\hat{j} + 2\hat{k}$ and $\vec{B} = 2\hat{i} + 3\hat{j} + \hat{k}$
Solution:
Given data:
- $\vec{A} = \hat{i} + 2\hat{j} + 2\hat{k}$
- $\vec{B} = 2\hat{i} + 3\hat{j} + \hat{k}$
As discussed above we know the formula of the dot product is
$\vec{A} \cdot \vec{B} = |\vec{A}| |\vec{B}| \cos\theta$
At first we need to find the value of $\vec{A} \cdot \vec{B}$
$\vec{A} \cdot \vec{B} = (1)(2) + (2)(3) + (2)(1) = 2 + 6 + 2 = 10$
Next, we will find the magnitude of $\vec{A}$ and $\vec{B}$ i.e $|\vec{A}|$ and $|\vec{B}|$
$|\vec{A}| = \sqrt{1^2 + 2^2 + 2^2} = \sqrt{9} = 3$
$|\vec{B}| = \sqrt{2^2 + 3^2 + 1^2} = \sqrt{14}$
Putting these value into the formula we get-
$10 = (3)(\sqrt{14}) \cos\theta$
$or\ \cos\theta = \frac{10}{3\sqrt{14}}$
$or\ \theta = \cos^{-1} \left( \frac{10}{3\sqrt{14}} \right)$
Find the projection of $\vec{A} = 3\hat{i} + 4\hat{j}$ on $\vec{B} = \hat{i}$
Solution:
We know the formula for the projection of $\vec{A}$ on $\vec{B}$ =
$$\frac{\vec{A} \cdot \vec{B}}{|\vec{B}|}$$
First we need to find the $\vec{A} \cdot \vec{B}$
$\vec{A} \cdot \vec{B} = (3)(1) + (4)(0) = 3$
Next find the $|\vec{B}|$
$|\vec{B}| = \sqrt{1^2 + 0^2} = 1$
$\text{Projection} = \frac{3}{1} = 3$
Check whether $\vec{A} = \hat{i} – \hat{j} + 2\hat{k}$ and $\vec{B} = 2\hat{i} + \hat{j} – \hat{k}$ are orthogonal.
Solution: We know that if two vectors are perpendicular i.e., the angle between them is 90°, they are orthogonal. And if the angle between two vectors is 90°, their dot product is always zero. So in this problem we need to check whether their dot product is zero or not.
$\vec{A} \cdot \vec{B} = (1)(2) + (-1)(1) + (2)(-1)$
$\vec{A} \cdot \vec{B} = 2 – 1 – 2 = -1$
We can see that their dot product is not zero, i.e. $\vec{A} \cdot \vec{B} \neq 0$. Therefore these two vectors are not orthogonal.