A vector is a mathematical entity that has both magnitude and direction. Vectors are used broadly in physics, engineering, computer science, and other fields. In this article we will discuss the different types of vectors:
Based on Magnitude and Direction
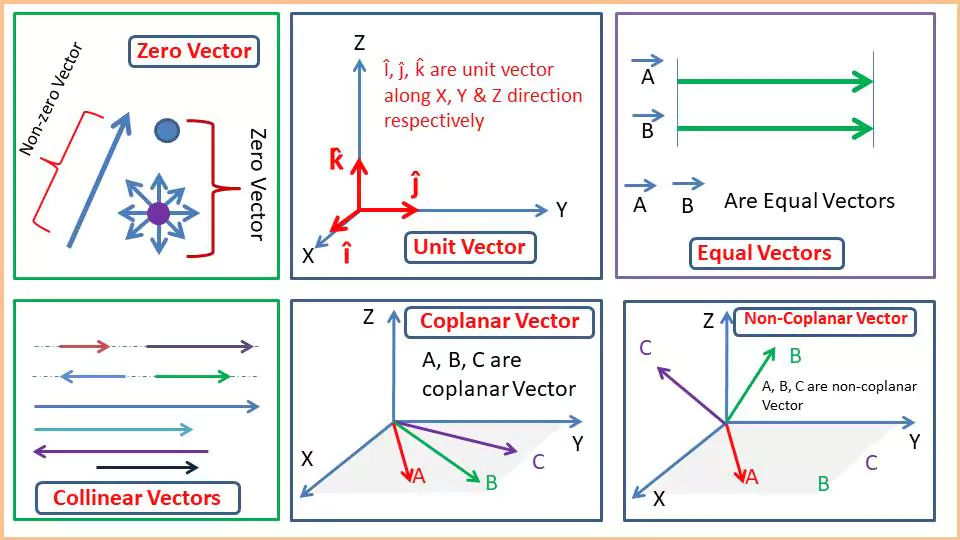
Zero Vector (Null Vector): A vector is said to be zero vector if it has zero magnitude. Zero vector has no specific direction because it has no magnitude or length. Symbol of zero vector- in 1 dimension: $\vec{0}=(0)$; in 2 dimension: $\vec{0}=\begin{bmatrix} 0 & 0 \end{bmatrix}$ and in 3-dimension: $\vec{0}=\begin{bmatrix} 0 & 0 &0 \end{bmatrix}$
Unit Vector: A unit vector has magnitude equal to 1. Unit vector is used to indicate direction. Unit vector is generally indicated by putting a ‘cap’ symbol on a letter. e.g. $\hat{n}$ and magnitude $\lVert\hat{n} \rVert$ = 1. If $\vec{A}$ is a vector then its unit vector can be calculated by dividing its magnitude $\lVert\vec{A} \rVert$ i.e. $\hat{n}$ = $\frac{\vec{A}}{\lVert\vec{A} \rVert}$
Equal Vectors: Two or more vectors are said to be equal vectors if they have the same magnitude and direction, irrespective of their initial points. In other words, equal vectors have same length same direction and are parallel. Thus $\vec{A}$ and $\vec{B}$ are parallel if $\lVert\vec{A} \rVert = \lVert\vec{B} \rVert$ and same direction.
Negative Vectors: Two vectors are said to be negative vectors if they have same magnitude but opposite directions. To find the negative of a vector, we need to multiply the given vector by -1. E.g. If $\vec{A}$ is a vector then its negative vector is $−\vec{A}$.
Based on Spatial Orientation
Collinear Vectors: Two or more vectors are said to be collinear if they lie along the same line or parallel lines. The magnitude can be different for these vectors. As collinear vectors are parallel to each other, they never meet or intersect.
Coplanar Vectors: Vectors that lie in the same plane in a 3-dimensional space are called coplanar vectors. Coplanar vectors are always linearly dependent and their scalar triple product is zero. This means, that if $\vec{A}$, $\vec{B}$, and $\vec{C}$ are coplanar then $\vec{A}\cdot (\vec{B}\times \vec{C}) = 0$.
Non-coplanar Vectors: If 3 or more vectors do not lie in the same plane, they are called Non-coplanar vectors. So $\vec{A}\cdot (\vec{B}\times \vec{C}) \neq 0$.
Based on Operations
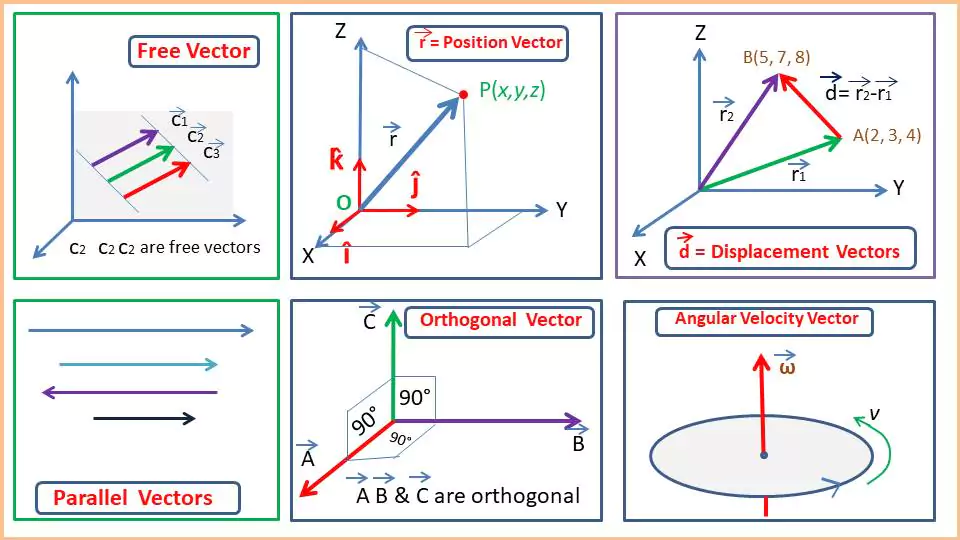
Free Vectors: Vectors that are not fixed to a specific point and can be moved parallel to themselves. A free vector is defined by its magnitude and direction, and not by its initial point.
Position Vectors: Position Vectors represent the position of a point in a coordinate system with respect to the center or origin. The position vector always starts from a fixed origin & $O(0,0,0)$ and ends at a position $P(x, y, z)$. If $P(x, y, z)$ is a point in the space of a 3-dimensional cartesian coordinate system, then $\overrightarrow{OP}$ represents the position vector of that point $P(x, y, z)$.
Position Vector $\overrightarrow{OP} = \vec{r} = \langle x, y, z \rangle \quad \text{or} \quad \vec{r} = x \hat{i} + y \hat{j} + z \hat{k}$
The magnitude of the position vector is $\lVert\vec{r} \rVert = \sqrt{x^{2}+y^{2}+z^{2}}$
Now if there are two points $P_{1} \left ( x_{1},y_{1},z_{1} \right )$ and $P_{2} \left ( x_{2},y_{2},z_{2} \right )$ in a rectangular coordinate system, then the position vector of point $P_{2}$ with respect to point $P_{1}$ is given by
$$\overrightarrow{{R_{P_{2}P_{1}}}} = \left ( x_{2}-x_{1} \right)\hat{i}+\left (y_{2}-y_{1} \right )\hat{j}+\left ( z_{2}-z_{1} \right )\hat{k}$$
The position vector $\vec{r}$ in polar coordinates is given as $\vec{r} = r \hat{e}_r$ where $\hat{e}_r$ is the unit vector in the radial direction.
The position vector is the most used vector in physics as it represents the position of a particle.
Sliding Vectors: Vectors that can slide along a specific line. In other words, vectors, that “slide” or shift along a particular line or direction, while maintaining their magnitude are called Sliding vectors. Consider a force of 10N acting at point A. The line of action of this force passes through another point B. In this case we can say that the force vector slide from point A to point B.
Bound Vectors: Vectors have a fixed initial point in space in space. Bound Vectors are also known as local vectors. These are defined by their specific point of application along with their magnitude and direction.
- A bound vector is attached to a specific point. It cannot be moved to another point.
- It has a well-defined magnitude and direction.
- If we consider a force of 10N at a fixed point P(2,3,4), then it can be considered as a bound vector.
Based on Physical Nature
Displacement Vector: A displacement vector is the shortest path between an initial point and a final point in a direction from an initial point to a final point.
The displacement vector is mathematically defined as $\vec{d}=\vec{r_2}−\vec{r_1}$ where $\vec{r_1}(x_1,y_1,z_1)$ and $\vec{r_2}(x_2,y_2,z_2)$ are the initial and final points respectively. The magnitude of this displacement vector is
$$|\vec{d}| = \sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2 + (z_2 – z_1)^2}$$
Info: Position vector is generally considered from the origin or center $O(0,0,0)$ of a coordinate system. While Displacement Vector is considered from one point $P_1(x_1,y_1,z_3)$ to another point $P_1(x_1,y_1,z_3)$.
Example: Suppose an object moves from point $A(2, 3, 4)$ to point $B(5, 7, 8)$.
Position Vectors are –
- $\vec{r}_1 = 2\hat{i} + 3\hat{j} + 4\hat{k}$
- $\vec{r}_2 = 5\hat{i} + 7\hat{j} + 8\hat{k}$
And the displacement vector is –
- $\vec{d} = \vec{r}_2 – \vec{r}_1 = (5 – 2)\hat{i} + (7 – 3)\hat{j} + (8 – 4)\hat{k}$
- or, $\vec{d} = 3\hat{i} + 4\hat{j} + 4\hat{k}$
Velocity Vector: It is a vector that describes the rate of change of the displacement vector. It has both magnitude (speed) and direction. The velocity vector $\vec{v}$ is define as
$$\vec{v} = \frac{d\vec{r}}{dt}$$
Acceleration Vector: It describes the rate of change of velocity. The acceleration vector $\vec{a}$ is define as
$$\vec{a} =\frac{d\vec{v}}{dt}=\frac{d^2\vec{r}}{dt^2}$$
Force Vector: It represents the magnitude and direction of a force. If $\vec{F}$ is a force vector then
$$\vec{F} = mass \times acceleration = m\cdot \vec{a}$$
Based on Components
Orthogonal Vectors: Two or more vectors are said to be orthogonal if they are mutually perpendicular to each other or form 90°. This means that their dot product is zero. Orthogonal vectors are always linearly independent. If $\vec{A}$ and $\vec{B}$ are orthogonal then,
$$\vec{A}\cdot \vec{B}= 0$$
$$|\vec{A}| |\vec{B}| cos\theta = 0$$
$$cos\theta = 0 \\or\ \theta = 90^{\circ}$$
Therefore we can say that the magnitude of the orthogonal vectors does not affect orthogonality—only the direction matters.
Parallel Vectors: If two vectors have the same direction or they are exactly opposite in direction, then they are called parallel vectors. The cross-product of two parallel vectors is always zero. Parallel vectors may vary by magnitude ($|\vec{A}| \neq |\vec{B}|$) but never intersect each other.
Mathematically, if $\vec{A}$ and $\vec{B}$ are two parallel vector then-
$$\vec{A} \times \vec{B}= 0$$
This gives $\theta = 0^{\circ}$ for same direction, or $\theta = 180^{\circ}$ for opposite direction.
On the other hand –
$$\vec{A} = k \vec{B}$$
Where $k$ is a scalar; If $k > 0$, the vectors point in the same direction. If $k < 0$; the vectors point in opposite directions.
Info: Parallel vectors are not always equal vectors, but equal vectors are parallel vectors.
Based on Usage in Mathematics and Physics
Row Vectors: A row vector is a (1 × 𝑛) matrix. This means it has a single row and multiple columns.
E.g. $\vec{R} = [r_1 \, r_2 \, r_3 \, \dots \, r_n]$
Column Vectors: A column vector is an (𝑛 × 1) matrix. This means it has a single column and multiple rows. E.g.-
$$\vec{C} =\begin{bmatrix} c_1 \\ c_2 \\ c_3 \\ \vdots \\ c_n \\ \end{bmatrix}$$
Gradient Vector: It represents the rate and direction of change in scalar fields. For a scalar function $f(x, y, z)$ the gradient is denoted by $\vec{\nabla} f$. It is defined as:
$$\vec{\nabla} f = \left( \frac{\partial f}{\partial x} \right) \hat{i} + \left( \frac{\partial f}{\partial y} \right) \hat{j} + \left( \frac{\partial f}{\partial z} \right) \hat{k}$$
Angular Velocity Vector: It represents angular velocity in rotational motion.
Electric Field Vector: It describes the direction and strength of the electric field at a point.
Magnetic Field Vector: It describes the direction and strength of the magnetic field at a point.
Based on usage in Physics, we have many more physical quantities which are vectors.