Derivation of Equation of Rectilinear Motion

The equations of motion describe the motion of an object in one dimension. These equations establish the relation between four physical quantities – displacement, velocity, acceleration, and time. The 4 equations of motion are

1. s = vt
2. v = u + at
3. s = ut + (1/2)at²
4. v² = u² + 2as.

Where-

1. s = displacement
2. u = initial velocity
3. v = final velocity
4. a = acceleration
5. t = time.

Characteristics of rectilinear motion.

1. The distance is equal to the magnitude of displacement.
2. The speed is equal to the magnitude of velocity.
3. Displacement, velocity and acceleration act in a straight line.
4. Though, displacement, velocity, and acceleration are vectors, the algebraic rule of addition and subtraction can be used instead of vector addition.

Assumptions

1. The object moves along a straight line (1D motion).
2. Acceleration (a) is constant.
3. Initial velocity (u), final velocity (v), displacement (s), and time (t) are the variables.

Derivation of s = vt

Algebraic Method

If there is no acceleration, then the velocity is uniform. Let a particle displace s with velocity v at a time t. According to the definition of velocity –

Particle displaces v at a time = 1 s.

Particle displaces 2v at a time = 2 s.

So the particle displaces vt at time = t s.

So s = vt

Another way

Velocity = displacement ÷ time

$$velocity = \frac{displacement}{time}$$

$$ or\ v = \frac{s}{t}$$

Rearranging

$$\text{s = vt}$$

Graphical Method

To establish the formula s = vt, consider the following figure-

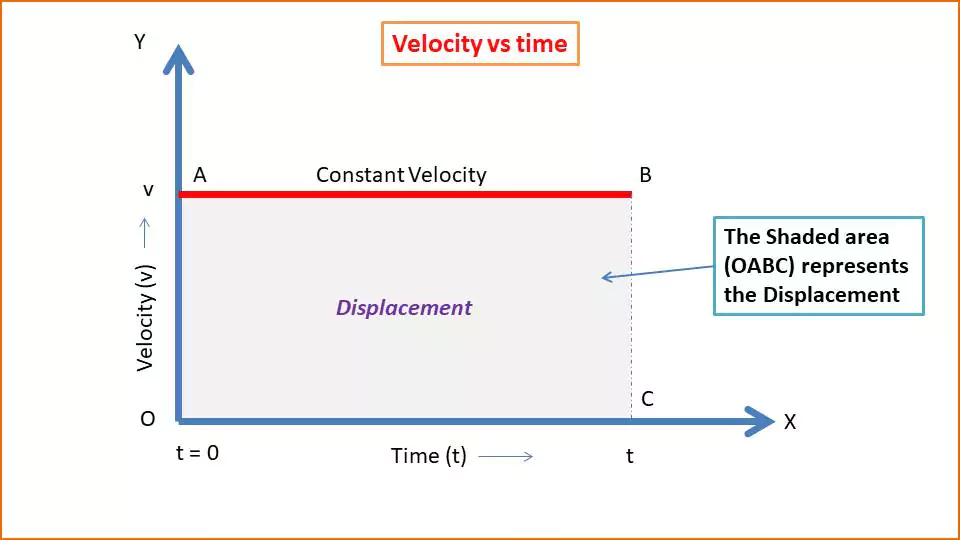
The velocity-time graph for uniform constant velocity is the parallel line to the time axis. Every point on the line AB represents the constant velocity. The area enclosed by the AB line with the time axis represents the displacement.

Displacement = area of the OABC rectangle.

S = Length × height

s = v × t

s = vt

Using Calculus

Mathematically, velocity is

$$v = \frac{ds}{dt}$$

$$ ds = v\cdot dt$$

integrating both sides

$$ \int_{0}^{s} ds = \int_{0}^{t} v\cdot dt$$

$$\int_{0}^{s} ds = v \int_{0}^{t} dt\ [\because v = constant]$$

$$ s = vt$$

Derivation of v = u + at

Algebraic Method

Let the initial velocity of an object be u. After time t the final velocity of the object is v.

∴ Change in velocity at time t = v – u.

So, the rate of change of velocity at a time t = (v – u)/t

According to the definition, the rate of change of velocity is called acceleration (a).

a = (v – u)/t

or, at = v – u

or, v = u + at

If the initial velocity of the particle is zero

then v = at

If the object moves with retardation, then

v = u – at

Graphical Method

Let us consider the initial velocity = u which is represented by OA = CD = u. After time t its velocity changes to v which is represented by CB = v.

Now tanθ = BD/AD = (CB – CD)/AB

tanθ = (v – u)/t [— equation 1]

tanθ = (change in velocity)/time

tanθ = rate of change of velocity

tanθ = acceleration = a [— equation 2]

Comparing equations 1 and 2 we get –

a = (v – u)/t

or, at = v – u

or v = u + at

Another way –

Here in this velocity-time graph, the velocity and time are represented along y and x axes respectively.

The equation of a straight line is

y = mx + c [— equation 3]

where y = final velocity = CB, x = time = t, and c is the distance from O to A i.e. c = OA = initial velocity = u.

Using these we get from equation 3,

v = u + at

Using Calculus

From the definition of acceleration –

$$a = \frac{dv}{dt}$$

For uniform acceleration, a = constant.

$$dv = a\cdot dt$$

Integrating both sides

$$\int_{u}^{v}dv = \int_{0}^{t}a\cdot dt$$

$$\int_{u}^{v}dv = a \int_{0}^{t} dt$$

$$[v]_u^v = a [t]_0^t$$

$$v − u = at$$

$$v = u + at$$

Derivation of s = ut + (1/2)at²

Algebraic Method

Let us consider the initial velocity of a particle is u. After time t its final velocity is v. The acceleration in this case is uniform i.e. a = constant.

For constant acceleration the average velocity

<v> = (u + v)/2

So the displacement = average velocity × time

s = (1/2) (u + v) × t

Putting v = u + at we get

s = (1/2) [u + ( u + at)] × t

s = (1/2) [2u + at)] × t

s = (1/2) (2u) × t + (1/2)at) × t

s = u + (1/2)at²

Graphical Method

To establish the formula s = u + (1/2)at² using graphical method, let us consider the following figure.

As we know the area covered by the velocity-time graph and the time axis gives the displacement.

So the displacement = area of trapezium OABC

Displacement (s) = area of rectangle OADC + triangle ABD

s = OA × OC + (1/2) AD × DB

s = OA × OC + (1/2) AD × AD× (DB/AD)

s = OA × OC + (1/2) AD²× (DB/AD)

DB/AD = tanθ = acceleration = a

s = OA × OC + (1/2) AD²× a

s = ut + (1/2)at²

Using Calculus

According to the definition of velocity v

$$v = \frac{ds}{dt}$$

Putting v = u + at

$$\frac{ds}{dt} = u + at$$

$$ds = u\cdot dt + at\cdot dt$$

Integrating both sides (at t = 0, s = 0 and t =t, s =s )

$$\int_{0}^{s}ds = u\cdot \int_{0}^{t}dt + a\int_{0}^{t}t\cdot dt$$

$$[s]_0^s = u\cdot [t]_0^t + a\cdot \frac{1}{2}[t^2]_0^t$$

$$s = ut + \frac{1}{2}at^2$$

Derivation of v² = u² + 2as

Algebraic Method

We established v = u + at. squaring both sides

v² = (u + at)²

v² = u² + 2 u.at + a²t².

v² = u² + 2a[ ut + (1/2)at²].

Putting the value of s = ut + (1/2)at²

v² = u² + 2as

Graphical Method

To establish s = ut + (1/2)at² , we again consider the figure again

We already discussed above that the tangent gives us the acceleration,

a = tanθ = BD/AD = BD/OC

and displacement s = area of trapezium OABC

area of trapezium OABC = (1/2) (OA + CB) × OC

So, a × s = (BD/OC) × [(1/2) (OA + CB) × OC]

a × s = (1/2) BD × (OA + CB)

a × s = (1/2) × (CB – CD) × (OA + CB)

a × s = (1/2) × (v – u) × (v + u)

a × s = (1/2) (v² – u²)

2 a × s = v² – u²

v² = u² + 2as

Using Calculus

$$a = \frac{dv}{dt}= \frac{dv}{ds}\cdot \frac{ds}{dt} = \frac{dv}{ds}\cdot v$$

$$ a ds = v dv$$

At time t = 0 the displacement s = 0 and initial velocity v = u. At time t, the displacement s =s and final velocity v= v. Integrating both sides with these limits,

$$a\int_{0}^{s}ds = \int_{u}^{v}v\cdot dv$$

$$a[s]_0^s = \frac{1}{2}[v^2]_u^v$$

$$2as = v^2 – u^2$$

$$ v^2 = u^2 + 2as$$

Derivation of s_n = u + (1/2)a(2n – 1)

The equation $s_n = u + \frac{1}{2}a(2n – 1)$ represents the displacement at the nth time or nth second.

displacement at nth second s_n = displacement at nth second minus displacement at (n-1)the second.

$ = (un + \frac{1}{2}an^2) – [u(n-1) + \frac{1}{2}a(n-1)^2]$

$ = (un + \frac{1}{2}an^2) – [(un-u) + \frac{1}{2}(an^2-2an + 1)]$

$un + \frac{1}{2}an^2 – un + u – \frac{1}{2}an^2 + an – \frac{1}{2}a$

$u + an – \frac{1}{2}a$

$s_n = u + \frac{1}{2}a(2n – 1)$