While going up and down in a lift, we feel that the weight of the body has increased slightly when the lift suddenly starts moving upwards. Conversely, when the lift suddenly starts moving downwards, the weight of the body seems to be slightly less. This is because-
When an object is placed on another object, the first object exerts a force on the second object due to its weight. Then the second object creates a reaction force. This reaction force is the weight of the first object. If the reaction increases for some reason, the weight of the object will be more and if the reaction decreases, the weight of the object will appear less.
The reaction increases or decreases due to the acceleration or deceleration of a moving lift. The reaction in the lift and the resulting effective weight of the object have been determined in some cases below.
Info: The apparent weight of a person in an elevator (lift) is the normal reaction force R which is exerted by the floor of the lift on the person.
Case-1: When the lift is moving upwards with acceleration ‘a‘:
Suppose an object of mass m is placed on the floor of the lift (see fig-1). The forces acting on the object are:
- The weight of the object W = mg (downwards)
- The upward reaction force R’.
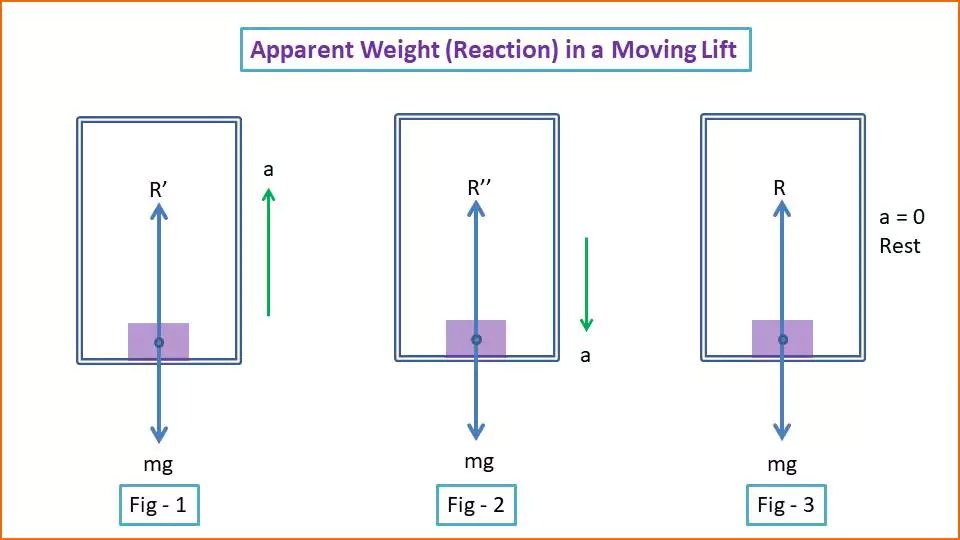
If the acceleration a is upwards then R’ − mg = ma
R’ = m(g + a)
Now we know that the reaction of the floor is the effective weight. So the weight of the object, W’ = m(g + a)
W’ = mg + ma
W’ > mg
So the reaction force acting on the object is greater than the weight W’ = mg. According to Newton’s third law, the object also exerts a downward force m(g + a) on the elevator floor. In this case, the weight increase is ma. So the object appears heavier.
Case-2: When the lift is moving downwards with acceleration a:
Suppose, in this case the reaction force (see fig-2) on the object is R”. Since the acceleration of the object ‘a‘ is downwards, then mg – R” = ma
R” = mg – ma = m(g−a)
R” < mg
That is, its weight on the object W = mg creates a reaction force less than mg. Therefore, the object feels lighter. The effective weight of the object W” = m(g – a)
Case-3: When the lift is stationary or moving upwards or downwards with constant Velocity:
When the lift is stationary or moving with constant Velocity, then its acceleration a = 0 (see fig-3) so the reaction on the object R = mg.
Therefore the magnitude of the force exerted by the object on the floor of the lift is equal to mg. Whether the lift goes up or down, if there is no acceleration of the lift then there will be no change in the apparent weight of the object.
Case-4: When the lift freely goes down (a = g)
If the elevator is descending without any obstacle (for example, if the elevator rope breaks), its acceleration a = g. Therefore, the reaction R = 0, that is, in this case, the elevator floor does not exert any upward force on the object. The object also does not exert any downward force on the elevator floor. Therefore, the object will be in a weightless state inside the elevator.
Case-5:. When the elevator descends with an acceleration greater than g.
Let us assume that somehow the elevator is kept moving downward with an acceleration greater than the gravitational acceleration (a > g). As soon as the elevator starts descending from the top, the contact between the floor and the object is severed. This is because although the acceleration of the elevator is a > g, the acceleration of the object descending is g. As a result, it can be seen that the object in the elevator is rising upwards and at some point the object will touch the roof of the elevator. Then the roof of the elevator exerts a downward reaction R1 on the rider.
So R1 + mg = ma
R1 = m(a – g)
Now it starts to move down from the contact with the roof of the elevator. According to the third law of motion, the object exerts an upward force m(a − g) on the roof of the elevator.
So in this case, the weight of the object m(a – g) acts upwards. This phenomenon is called ‘superweight-lessness‘.
Summary of Apparent Weight in a Lift
| Lift Condition | Acceleration a | Apparent Weight R |
|---|---|---|
| Lift at Rest or Constant Velocity | a = 0 | R = mg |
| Lift Accelerating Upward | a > 0 | R = m(g+a) (Heavier) |
| Lift Accelerating Downward | a < 0 | R = m(g−a) |
| Lift in Free Fall | a = g | R = 0 (Weightless) |
| Lift fall with a > g | a > g | R = m(a – g) (superweight-lessness) |