Acceleration

Acceleration is a physical quantity that measures how quickly the velocity of an object changes. When the velocity of an object does not remain the same over time, we can say that there exists an acceleration on the object. For increasing velocity, there exists acceleration and for decreasing velocity, there exists retardation. As velocity is a vector, acceleration is also a vector.

Now Imagine a car is stopped in traffic that shows a red light. Here the initial velocity of the car is 0 m/s. When the light turns green, the car begins to move forward. The velocity of the car increases here and we can say acceleration is produced. This increase in velocity is called acceleration.

How much acceleration is created? Let’s say the velocity of the car reaches 10 m/s after 5 seconds. The acceleration is calculated by measuring the velocity changes divided by the time taken to reach the final velocity. So the acceleration is (10 m/s – 0 m/s) / 5 s = 2 m/s².

Definition

The rate of change of velocity with respect to time is called acceleration.

Acceleration is a vector quantity that describes the change in an object’s velocity.

Mathametically, acceleration is the first derivative of velocity with respect to time

Formula

If a = acceleration, Δv = change in velocity, Δt = time interval, then the formula of acceleration is given by –

$$a = \frac{\Delta v}{\Delta t}$$

i.e.

$$\text{acceleration} = \frac{\text{change in velocity}}{\text{time}}$$

• If a = Positive (+), we may call positive acceleration or simply acceleration.
• If a = Negative (−), we call this negative acceleration or deacceleration or retardation.

Unit

$$\text{acceleration} = \frac{\text{velocity}}{\text{time}}$$

so

$$\text{unit of acceleration} = \frac{\text{unit of velocity}}{\text{ unit of time}}$$

$$\text{unit of acceleration} = \frac{\frac{\text{unit of displacement}} {\text{unit of time}}}{\text{ unit of time}}$$

$$\text{unit of acceleration} = \frac{\text{unit of displacement}}{\text{ unit of time}^2}$$

• In SI or MKS system the unit of acceleration is meter per second² or m/s² or m.s⁻².
• In CGS system the unit of acceleration is centimeter per second² or cm/s² or cm.s⁻².
• In FPS system the unit of acceleration is foot per second² or ft/s² or ft.s⁻².

Dimension

$$\text{dimension of acceleration} = \frac{\text{dimension of velocity}}{\text{ dimension of time}}$$

$$\text{dimension of acceleration} = \frac{\text{[LT }^{-1} ]}{\text{ [T]}}$$

$$\text{dimension of acceleration} = \text {[LT}^{-2}]$$

Types of Acceleration

Uniform Acceleration

Uniform acceleration means the acceleration remains the same throughout its motion. This happens when the change in velocity remains constant over time. Suppose v_a v_b v_c and v_d are different increased velocities at points A, B, C and D respectively in the equal interval of time t. Then if (v_b − v_a) = (v_c − v_b) = (v_d − v_c) over the equal interval of time, then the acceleration will be called uniform. This means If an object undergoes uniform acceleration, its acceleration a is constant, mathematically,

$$a = \frac{v_f – v_i}{t} = \text{constant}$$

Example: Freely falling objects have uniform gravitational acceleration g = 9.8 m/s². The motion of a ball rolling down in an inclined plane has constant acceleration.

Non-uniform Acceleration

Non-uniform Acceleration means the acceleration does not remain the same throughout its motion. This happens when the change in velocity does not remain constant over time. Suppose v_a v_b v_c and v_d are different increased velocities at points A, B, C and D respectively in the equal interval of time t. Then if (v_b − v_a) ≠ (v_c − v_b) ≠ (v_d − v_c) over the equal interval of time, then the acceleration will be called non-uniform. This means If an object undergoes non-uniform acceleration, its acceleration a is not constant, mathematically,

$$a = \frac{v_f – v_i}{t} \not = \text{constant}$$

Example: A car moving in traffic suddenly stops and speeds up, A rocket launching into Space, etc are examples of Non-uniform Acceleration.

Average Acceleration

The acceleration of a moving object does not remain the same for the instant. If we divide the difference between initial and final velocity by total time, we get the average acceleration. Mathematically, the average acceleration

$$\left< \vec{a}\right> = \frac{v_{\text{final}}- v_{\text{initial}} }{t}$$

$$or\ \left< \vec{a}\right> = \frac{{v_f} – {v_i}}{{t_f} – {t_i}}$$

$$or\ \left< \vec{a}\right> = \frac{\Delta v}{\Delta t}$$

Instantaneous Acceleration

The Acceleration of an object at a particular instant of time is called Instantaneous Acceleration.

To understand this let a the difference of the velocity of a particle be Δv at the interval of time between t to (t+Δt). Mathematically, acceleration $a$ is

$$a\ = \frac{\Delta v}{\Delta t}$$

If we decrease the time interval, the velocity difference of the particle will also decrease. Also if the value of Δt tends to zero, the value of Δv will tend to zero. In this situation, the limiting value of the acceleration is called the instantaneous acceleration. Mathematically

$$\vec{a}_{\text{inst}} = \lim_{\Delta t \to 0} \frac{\Delta \vec{v}}{\Delta t}$$

or, using differentiation

$$\vec{a}_{\text{inst}} = \frac{d\vec{v}}{dt} $$

Relation between acceleration and displacement:

$$\vec{a} = \frac{d\vec{v}}{dt} = \frac{d}{dt}(\frac{d\vec{s}}{dt})= \frac{d^2\vec{s}}{dt^2}$$

Velocity-Time Graph

The figure given below shows the velocity vs time graph.

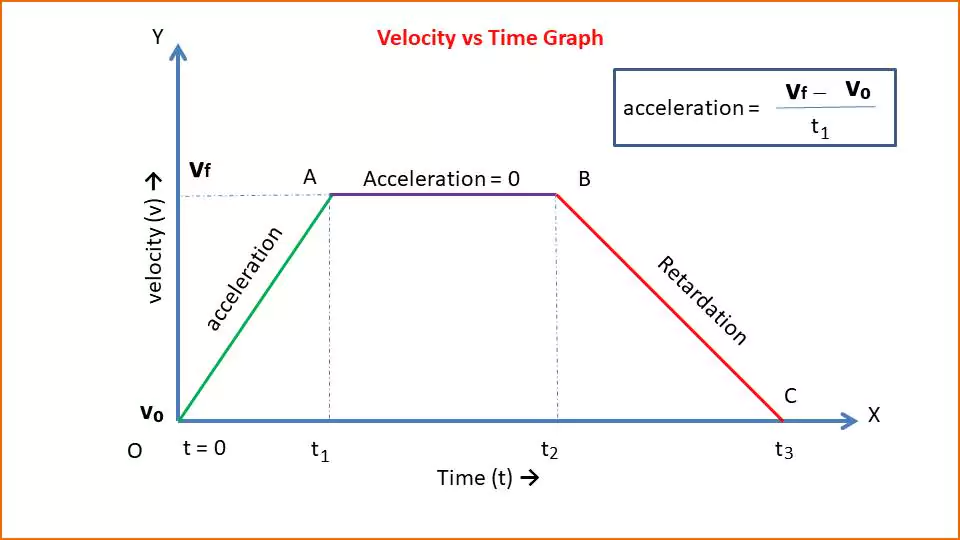
At point O, velocity is v₀ and at point A, velocity is v_f. The OA line shows velocity changing uniformly over time t₁. So line OA represents the uniform acceleration.

From point A to B the velocity is not changing over time. So line AB does not represent acceleration.

From time t₂ to t₃, the velocity is uniformly decreasing. Here as the velocity decreases the acceleration is negative i.e. BC line represents retardation.

Info: The constant slope in the velocity vs time graph represents uniform acceleration.

Displacement vs time

The figure given below shows the displacement vs time graph.

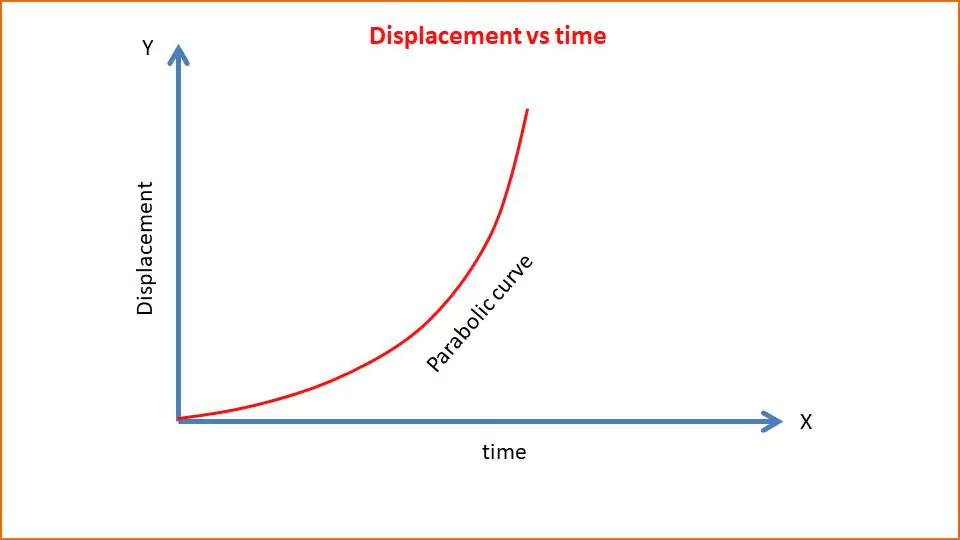
The displacement vs time graph is a parabolic curve that represents that the velocity is not uniform, but increasing continuously. So as the displacement vs time graph is parabolic, it represents acceleration.

Info: As displacement increases non-linearly with time there exists acceleration.

Problems Solutions