Displacement

The change in position in a particular direction of a particle is known as Displacement.

Definition: The shortest straight-line distance between the initial and final positions of the object, along with the direction is called displacement.

Displacement is a vector quantity as it has both the magnitude and a particular direction.

It is important to note that distance measures the total path traveled by a particle while displacement is only the overall change in position along a fixed direction.

Info: The displacement helps to describe the motion of a particle more accurately as it considers both direction and the shortest path. It is essential to calculate velocity, acceleration, and other vector quantities.

To understand the displacement let us consider the following figure.

In Figure (1.1), a particle is moving from point O to point A in four different paths – paths (I), (II), (III) and (IV). Among them, the red path (I) is the shortest and has a particular direction from O to A. So the red Path (I) here represents the displacement and the other three paths (II), (III) and (IV) represent distance as they do not have a fixed direction.

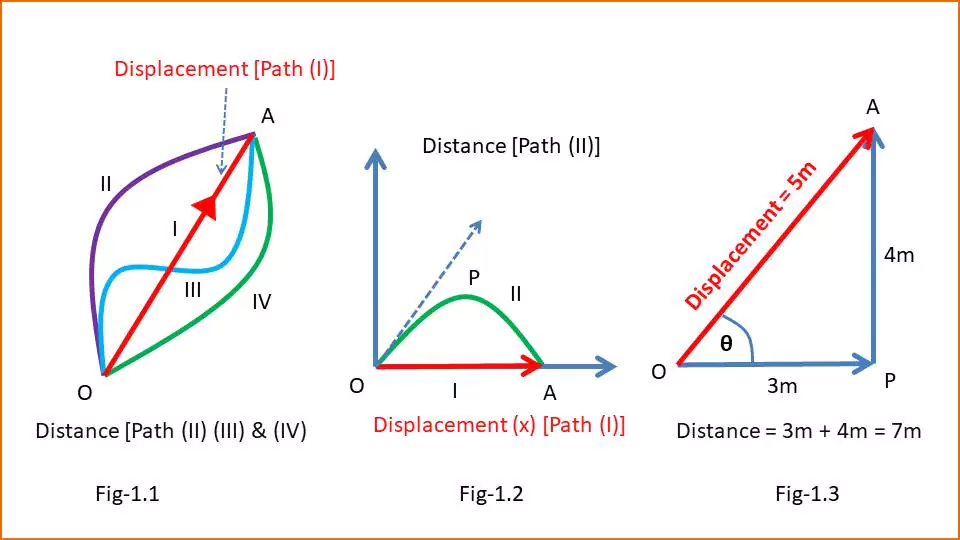
In Figure (1.2), a particle is projected along OP and reaches the ground at point A. In this case the particle covers OPA distance (parabolic path) and OP displacement (in the direction from point O to point A).

In Figure (1.3), a particle initially goes from point O to Point P horizontally and thereafter goes to Point A vertically. In this case the distance covered by the particle is (3m + 4m) = 7m. However, its displacement is not 5m but can be calculated geometrically.

Displacement = $\overrightarrow{OA} = \sqrt{3^2+4^2} = 5m$ along point O to point A. And its direction is given by angle θ.

$$\theta = tan^{-1}(\frac{4}{3})$$

Therefore, the displacement of an object does not depend on how it moves from one position to another. That is, the displacement is not path-dependent but only depends on the initial and final positions of the object.

Info: Displacement can be positive, negative, or zero depending on direction while distance is always positive or zero.

Unit: C.G.S unit of displacement is - centimeter (cm) and the SI unit is - meter (m).

Dimension: The dimension of displacement is [L].

Zero displacement: If the initial and final positions of an object are the same, then its displacement is zero. That is, if a person starts from one place and walks some distance and then returns to the same place, then his displacement is zero. After throwing an object vertically upwards from the surface of the earth, the object rises a little and then returns to the surface. In this case, the displacement of that object is zero. So it can be seen that even if a particle covers some distance, its displacement can be zero. It is noted that zero displacement does not have a specific direction.

From the above discussion we can conclude that the displacement is always less than or equal to distance.

$$Displacement \leq Distance$$

Geometrical Representation of Displacement

In a 2-dimensional and 3-dimensional cartesian coordinate, we can represent the magnitude and direction of displacement.

2D representation

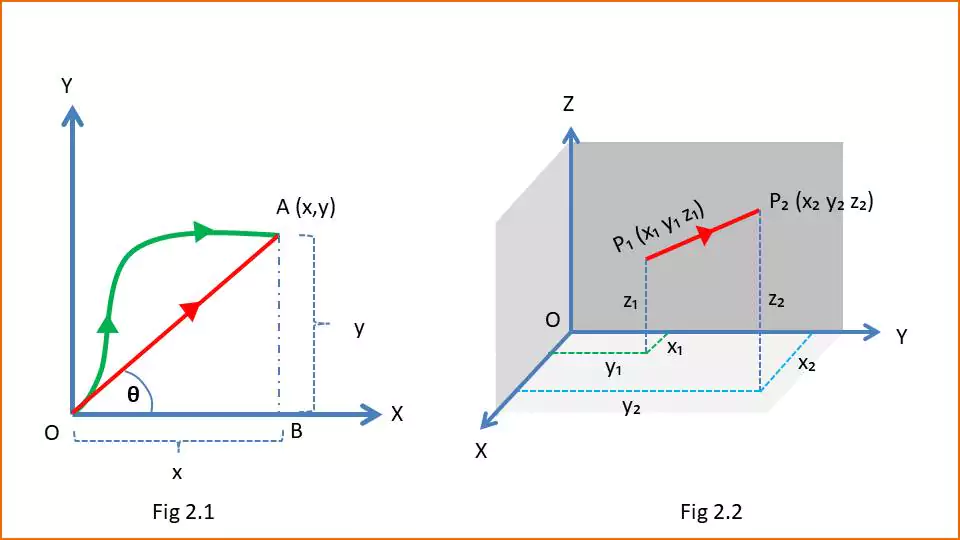
In a 2D Cartesian coordinate system there are two axises x and y. Let a particle is moving from point O to point A (figure 2.1). The coordinate of point A is (x,y). The length of the line OA represents the magnitude of displacement. If $|\overrightarrow{OA}|$ represents the magnitude of the displacement then –

$$ |\overrightarrow{OA}| = \sqrt{x^2+y^2}$$

Its direction is given by the angle θ made with the x-axis.

$$\theta = tan^{-1}(\frac{y}{x})$$

3D representation

In a 3-D cartesian coordinate system there are three mutually perpendicular axises x, y and z. Let a particle moves from point P₁(x₁,y₁,z₁) to point P₂(x₂,y₂,z₂) [figure 2.2]. Here the displacement is represented by $\overrightarrow{P_1P_2}$. If $|\overrightarrow{P_1P_2}|$ denotes the magnitude of the displacement then –

$$|\overrightarrow{P_1P_2}| = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2+ (z_2-z_1)^2}$$

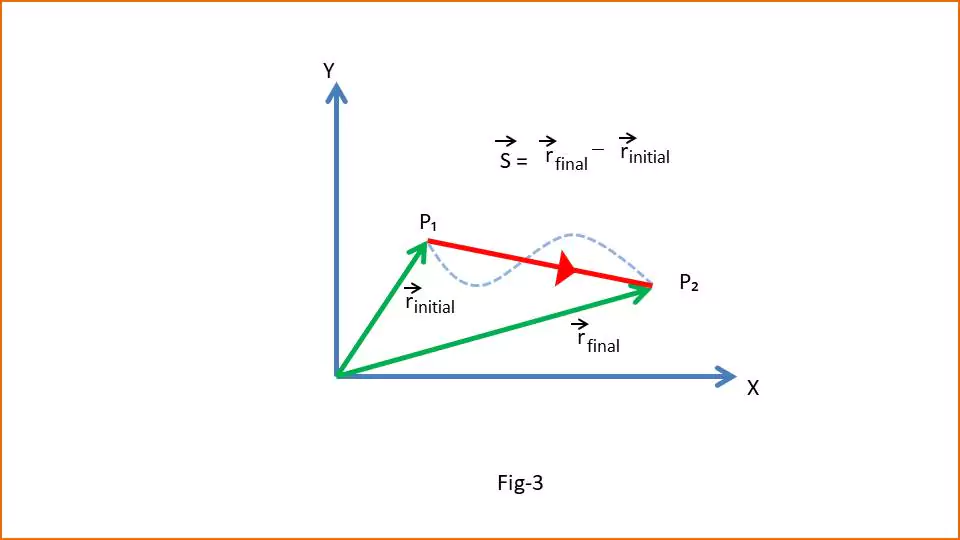
Mathematically displacement is represented by –

$$\vec{s} = \vec{r}_{final} -\ \vec{r}_{initial}$$

• Where $\vec{s}$ = Displacement;
• $\vec{r}_{initial}$ = initial position;
• $\vec{r}_{final}$ = final position.

Example-1: To understand the displacement let us consider the following figure-4.

Solution:

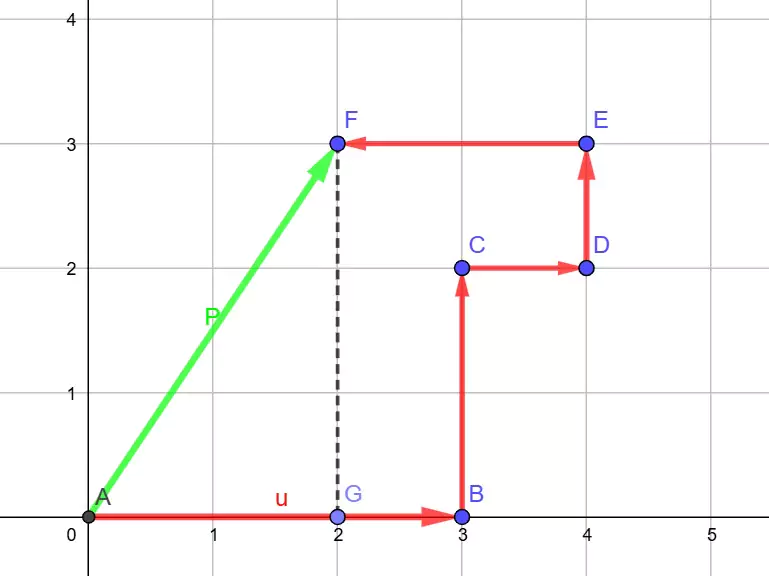
A person starts moving from point A to point B. Next, he goes to point C. After he reaches point F through point D and point E.

Total distance is = (3 + 2 + 1 + 1 + 2) = 9 units.

However, the magnitude of the displacement is the length of AF line.

$$|\overrightarrow{AF}| = \sqrt{1^2+3^2} = \sqrt{10} \ units$$