Whether an object is stationary or moving is always considered with respect to another object. With respect to which the motion of an object is considered, is called the reference frame. The velocity of a moving object is expressed with respect to this frame of reference. Again, no frame of reference is absolutely fixed. Therefore, the absolute motion of an object cannot be determined.
We generally express the velocity of an object with respect to the Earth. Since the Earth is not fixed, when we mention the velocity of an object, it is actually only the relative velocity with respect to the earth – it is not the absolute velocity.
Relative velocity is the velocity of one object as observed from another object. It tells us how fast one object is moving with respect to the other object.
Definition of Relative Velocity: The velocity of one moving object with respect to another moving or stationary object is called relative velocity.
Info: Relative velocity depends on the reference frame we choose.
Examples of Relative velocity:
- Let us suppose that two trains are moving parallel to each other at the same speed and in the same direction. When two passengers of the two trains look at each other through the windows, both of them will feel that no one is moving. They will consider each other as stationary. In this case, it can be said that the relative velocity of one passenger with respect to the other is zero.
- If one train is moving faster than the other, the passenger of the faster train will think that the slower train is moving in the opposite direction. In fact, both are moving in the same direction. This opposite velocity of the slower train is its relative velocity with respect to the first train. Conversely, the relative velocity of the first train with respect to the second train is forward.
- Trees, houses, etc. on the roadside appear to be moving in the opposite direction from the moving car. But they are not moving. This is the relative speed of the trees and houses with respect to the passenger in the car.
- If there is no wind, a stream of rain falls vertically on a pedestrian standing on the road. Now when the person starts moving on the road, the stream of rain falls on his face from the front (making an angle). This speed of rain is the relative speed with respect to the pedestrian.
General Formula of Relative Velocity
Let us consider two moving objects A and B. The velocity of A is $\overrightarrow{V_A}$ and velocity of B is $\overrightarrow{V_B}$.
The relative velocity of A with respect to B is $\overrightarrow{V_{AB}}$ = velocity of A − velocity of B.
$$\begin{gather} \overrightarrow{V_{AB}} = \overrightarrow{V_A} − \overrightarrow{V_B} \end{gather}$$
Similarly, The relative velocity of B with respect to A is $\overrightarrow{V_{BA}}$ = velocity of B − velocity of A.
$$\begin{gather} \overrightarrow{V_{BA}} = \overrightarrow{V_B} − \overrightarrow{V_A} \end{gather}$$
Relative Velocity in 1-Dimension
Case-1: When both objects A & B move in the same direction (θ = 0):
If A and B move in the same direction, then the above formula remains the same. i.e. the velocity of A with respect to B is $\overrightarrow{V_{AB}} = \overrightarrow{V_A} − \overrightarrow{V_B}$. And the velocity of B with respect to A is $\overrightarrow{V_{BA}} = \overrightarrow{V_B} − \overrightarrow{V_A}$. In this case the relative velocity is the difference between two velocities.

Now if the velocities of A and B are same; i.e. $|\vec{V_A}| = |\vec{V_B}|$, their relative velocity is $\vec{V_{AB}} = \vec{V_A} − \vec{V_B} = 0$
Info: If objects move in the same direction, their relative velocity decreases.
Example: Car A is moving at $\vec{V}_A$ = 60 km/h, and another car B is moving at $\vec{V}_B$ = 40 km/h, both in the same direction. The relative velocity of car A w.r.t car B is
$\vec{V}_{AB} = \vec{V}_A – \vec{V}_B = 60 – 40 = 20 \, \text{km/h}$
So car A appears to move at 20 km/h relative to car B.
Case-2: When both objects A & B move in the opposite direction (θ = 180):
Here two objects are moving in opposite directions, so we can consider the velocity of A to be $\overrightarrow{V_A}$ and velocity of B to be $− \overrightarrow{ V_B}$.
The relative velocity of A with respect to B is –
$$\overrightarrow{V_{AB}} = \overrightarrow{V_A} − (− \overrightarrow{V_B}) $$
$$\begin{gather} \overrightarrow{V_{AB}} = \overrightarrow{V_A} + \overrightarrow{V_B} \end{gather}$$
Now if the velocities of A and B are same; i.e. $|\vec{V_A}| = |\vec{V_B}|$, their relative velocity is $\vec{V_{AB}} = (\vec{V_A} + \vec{V_B}) = 2\vec{V_A} $ which is double.
The relative velocity of B with respect to A is
$$ \overrightarrow{V_{BA}} = − \overrightarrow{V_B} − \overrightarrow{V_A}$$
$$\begin{gather} \overrightarrow{V_{BA}} = − (\overrightarrow{V_B} + \overrightarrow{V_A}) \end{gather}$$
Info: If objects move in opposite directions, their relative velocity increases.
Example: Car A is moving at $\vec{V}_A$ = 60 km/h, and another car B is moving at $\vec{V}_B$ = 40 km/h, in the opposite direction. The relative velocity of car A w.r.t car B is
$\vec{V}_{AB} = \vec{V}_A + \vec{V}_B = 60 + 40 = 100 \, \text{km/h}$
Here So car A appears to move at 100 km/h relative to car B.
Relative Velocity in 2-Dimension
Case-3: When Two objects A & B start moving in different directions.
In this case, A and B moving in different directions from a common point. The relative velocity of one from another is calculated by vector subtraction (eqn-1).
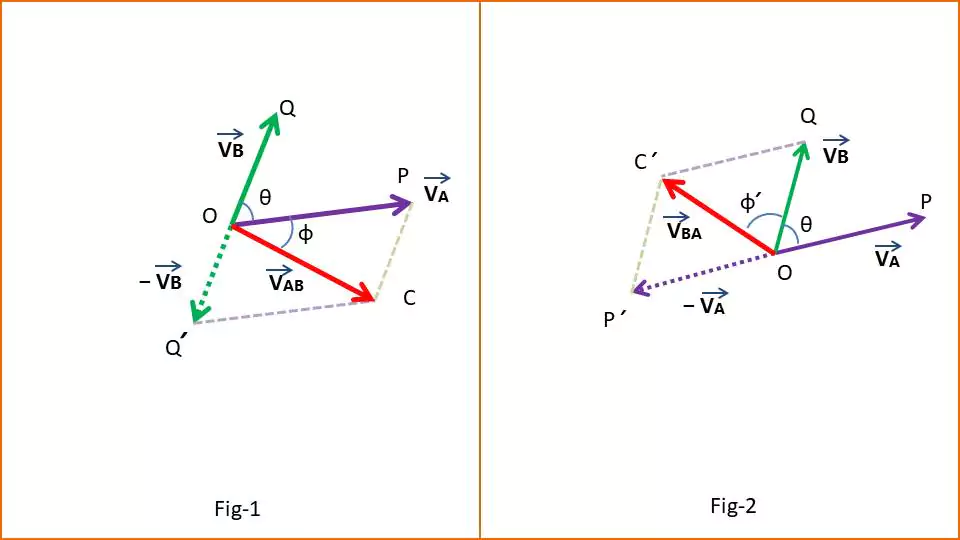
Two objects A and B are moving along OP and OQ with velocity $\overrightarrow{V_A}$ and $\overrightarrow{V_B}$ respectively. The angle between $\overrightarrow{V_A}$ and $\overrightarrow{V_B}$ is θ. We need to find the relative velocity of A with respect to B. For this the OQ is extended in the opposite to OQ’ so that OQ = OQ’ and $\overrightarrow{OQ’} = − \overrightarrow{V_B}$ (Image-2 fig-1).
Therefore according to the parallelogram law of vector addition, the diagonal OC of parallelogram OPCQ’ will represent the relative velocity of A w.r.t B.
The angle between OP and OQ’ is (180 − θ).
$|\vec{V_{AB}}|^{2} = |\vec{V_A}|^{2} + |\vec{V_B}|^{2} + 2\cdot |\vec{V_A}| \cdot |\vec{V_B}| \cdot cos (180-\theta )$
As $cos (180-\theta ) = -cos \theta$
$|\vec{V_{AB}}|^{2} = |\vec{V_A}|^{2} + |\vec{V_B}|^{2} – 2\cdot |\vec{V_A}| \cdot |\vec{V_B}| \cdot cos \theta$
$$\begin{equation} \end{equation}$$
The direction of the object A with respect to B is given by angle ϕ. This means that an observer moving along OQ with velocity VB will see that object A is moving along OQ’ with velocity VAB. The angle ϕ is given by –
$$tan\phi = \frac{V_B\cdot sin (180 – \theta )}{V_A + V_B\cdot cos(180-\theta )}$$
As $sin (180\ -\ \theta ) = sin \theta $
$$\begin{equation} tan\phi = \frac{V_B\cdot sin \theta}{V_A\ -\ V_B\cdot cos\theta} \end{equation}$$
To find the relative velocity of B w.r.t A we consider the fig-2 (of image-2) of the above-given image.
Here we extend OP to P’ so that OP = OP’ and $\overrightarrow{OP’} = − \overrightarrow{V_A}$.
So the diagonal of the parallelogram OQC’P’ will represent the relative velocity of B w.r.t A. Appling the parallelogram law of vector addition we get the relative velocity of B w.r.t. A is –
$$|\vec{V_{BA}}|^{2} = |\vec{V_A}|^{2} + |\vec{V_B}|^{2} – 2\cdot |\vec{V_A}| \cdot |\vec{V_B}| \cdot cos \theta$$
$$\begin{equation} \end{equation}$$
and the angle along the relative velocity of B will be observed with respect to A is given by ϕ’.
$$\begin{equation} tan\phi ‘ = \frac{V_B\cdot sin \theta}{V_A\ -\ V_B\cdot cos\theta} \end{equation}$$
From equations (5) and (7), we see that the magnitude of relative velocity remains the same i.e. $|\vec{V_{AB}}|=|\vec{V_{BA}}|$
Now if θ = 0; $\overrightarrow{V_{AB}} = \overrightarrow{V_A} − \overrightarrow{V_B}$ which is equation (1) of case-1.
$$|\vec{V_{AB}}|^{2} = |\vec{V_A}|^{2} + |\vec{V_B}|^{2} – 2\cdot |\vec{V_A}| \cdot |\vec{V_B}| \cdot cos 0 $$
$$ = |\vec{V_A}|^{2} + |\vec{V_B}|^{2} – 2\cdot |\vec{V_A}| \cdot |\vec{V_B}| \cdot 1 $$
$$ = \bigg(|\vec{V_A}| – |\vec{V_B}|\bigg)^{2}$$
$$ or\ \overrightarrow{V_{AB}} = \overrightarrow{V_A} − \overrightarrow{V_B}$$
And if θ = 180; $cos180 = -1$; $\overrightarrow{V_{AB}} = \overrightarrow{V_A} + \overrightarrow{V_B}$ which is equation (2) of case-2.
$$|\vec{V_{AB}}|^{2} = |\vec{V_A}|^{2} + |\vec{V_B}|^{2} – 2\cdot |\vec{V_A}| \cdot |\vec{V_B}| \cdot cos 0 $$
$$ = |\vec{V_A}|^{2} + |\vec{V_B}|^{2} – 2\cdot |\vec{V_A}| \cdot |\vec{V_B}| \cdot (-1) $$
$$ = \bigg( |\vec{V_A}| + |\vec{V_B}|\bigg)^{2}$$
$$ or\ \overrightarrow{V_{AB}} = \overrightarrow{V_A} + \overrightarrow{V_B}$$
Applications of Relative Velocity
- Finding the effective velocity of a boat moving in a river with a stream.
- Calculating the angle at which a person should hold an umbrella when walking or running in the rain.
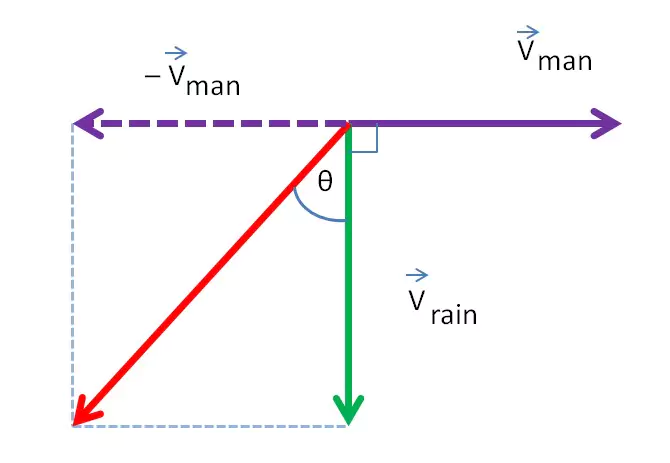
A man is walking with a velocity of 4 m/s in the east. Rain is falling vertically downward with a velocity of 6 m/s. At what angle should the man hold his umbrella to avoid getting wet?
Solution: Given velocity of the man is $\vec{V_{man}}$ = 4 m/s along east, and velocity of rain is $\vec{V_{rain}}$ = 6 m/s along downward.
Clearly the angle between the velocity of man and the velocity of rain is 90.
The relative velocity of rain with respect to the man is
$$\vec{V_{rain/man}} = \vec{V_{rain}} − \vec{V_{man}}$$
$|\vec{V_{rain/man}}|^{2} = |\vec{V_{rain}}|^{2} + |\vec{V_{man}}|^{2} – 2\cdot |\vec{V_{rain}}| \cdot |\vec{V_{man}}| \cdot cos 90 ^{\circ}$
$|\vec{V_{rain/man}}|^{2} = |\vec{V_{rain}}|^{2} + |\vec{V_{man}}|^{2} – 2\cdot |\vec{V_{rain}}| \cdot |\vec{V_{man}}| \cdot (0)$
$|\vec{V_{rain/man}}|^{2} = |\vec{V_{rain}}|^{2} + |\vec{V_{man}}|^{2}$
$|\vec{V_{rain/man}}| = \sqrt{|\vec{V_{rain}}|^{2} + |\vec{V_{man}}|^{2}}$
$|\vec{V_{rain/man}}| = \sqrt{4^{2} + 6^{2}}$
$|\vec{V_{rain/man}}| = \sqrt{16 + 36}$
$|\vec{V_{rain/man}}| = \sqrt{52}$
The angle (θ) of the umbrella with the vertical is given by:
$$tan\theta= \frac{V_{man}\cdot sin (180 – 90 )}{V_{rain} + V_{man}\cdot cos(180 – 90 )}$$
$$tan\theta= \frac{V_{man}\cdot sin (90 )}{V_{rain} + V_{man}\cdot cos(90 )}$$
$$tan\theta= \frac{|V_{man}|}{|V_{rain}|}$$
$$\tan \theta = \frac{4}{6} = \frac{2}{3}$$
$$\theta = \tan^{-1}\left(\frac{2}{3}\right)$$
$$\theta \simeq 33.7^{\circ}$$
Alternate Method
We can solve this problem using basis vectors $\hat{i}$ and $\hat{j}$.
The velocity of man and rain can be considered as $\vec{V_{man}} = 4\hat{i}$ and $\vec{V_{rain}} = 6\hat{j}$
$\vec{V}_{\text{rain/man}} = -4\hat{i} + 6\hat{j}$
And the angle θ of the rain with the vertical is given by-
$$tan\theta= \frac{|V_{man}|}{|V_{rain}|}$$
$$\tan \theta = \frac{4}{6} = \frac{2}{3}$$
$$\theta \simeq 33.7^{\circ}$$