Cross Product or Vector Product of Vectors

We know that vectors have both magnitude and direction. For having a specific direction, their product is not as simple as algebraic multiplication – that means the product of two vectors is completely dependent on their alignment or direction. There are two types of vector products – one is scalar product and another is vector product. The scalar product (also called dot product) gives scalar and the vector product (also known as cross product) gives vector.

The vector product is represented by a “cross” i.e. “×” between two vectors – for that it is called Cross product. If $\vec{A}$ and $\vec{B}$ are two vectors, their cross product is represented by $\vec{A}\times \vec{B}$.

Definition: The cross product is a mathematical operation (a type of multiplication) that takes two vectors and returns a vector quantity in three-dimensional space.

Significance of Cross Product

The physical significance of cross product is that it gives the area of a parallelogram whose two adjacent sides are formed by two vectors. This means if we perform a cross product of two vectors, then the magnitude of this operation gives the area of the parallelogram with the two adjacent sides represented by those two vectors. Also, the orientation of the cross product is perpendicular to the plane form by those two vectors. The direction of the cross product is determined by the right-hand thumb rule. So we can say that the cross product gives the area vector which is orthogonal to both of those two vectors. To understand and visualize this fact, consider the following example.

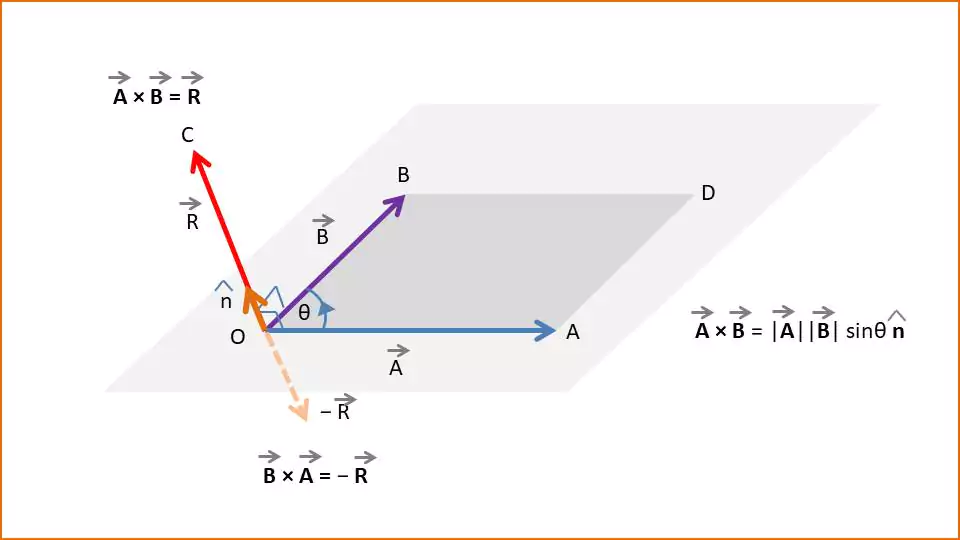
Let $\vec{A}$ and $\vec{B}$ represent two vectors which are two adjacent sides of the parallelogram OADB. The magnitude of the cross product of $\vec{A}$ and $\vec{B}$ gives the area of the parallelogram OBDB. That is the Area of parallelogram OADB = $|\vec{A}\times \vec{B}|= |\vec{A}| |\vec{B}| \sin\theta$; And the orientation of the resultant vector $\vec{R}$ is along the OC.

$\text{Area of the parallelogram} = |\vec{A}||\vec{B}|\sin\theta$

Direction of Cross Product

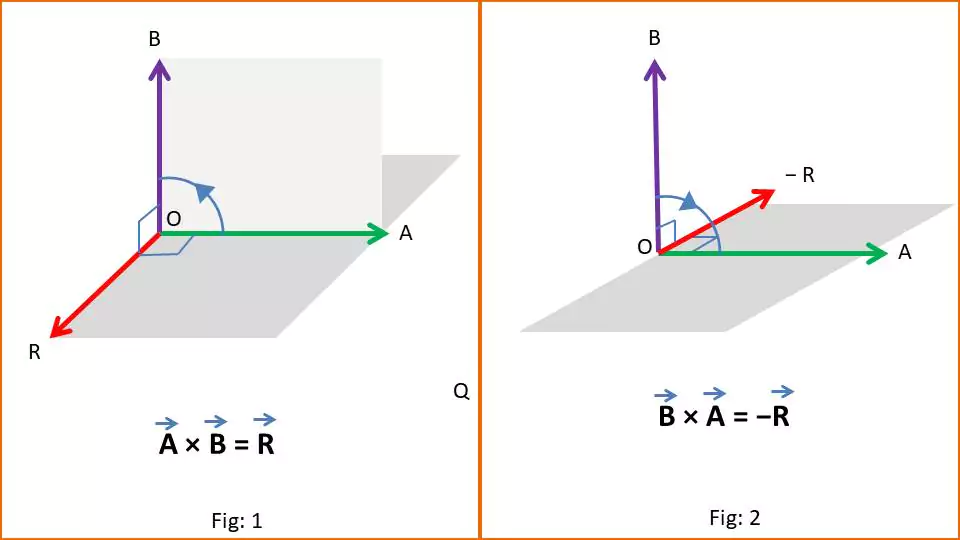
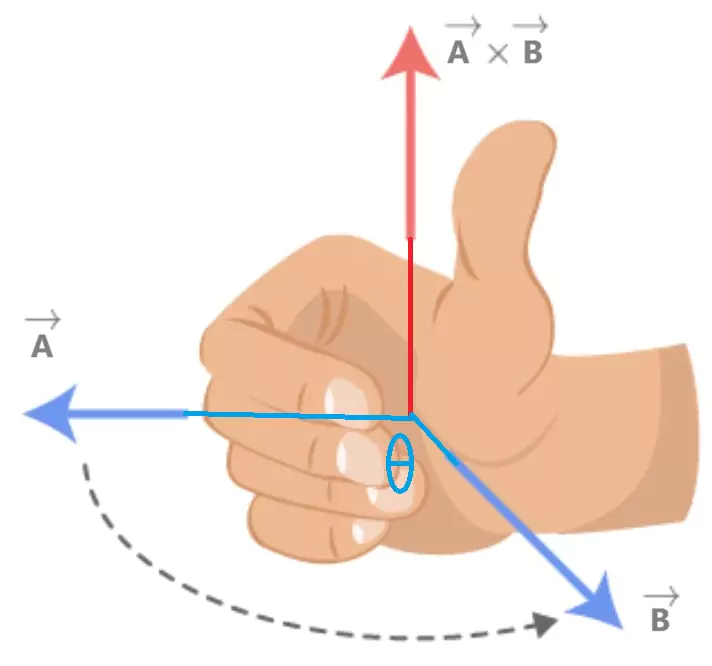
The direction of the cross product of two vectors is perpendicular (i.e. 90°) to both vectors following the right-hand thumb rule. To find the direction of $\vec{A} \times \vec{B}$ we need to keep our left-hand palm on the first vector ($\vec{A}$) and sweep the palm towards the second vector ($\vec{B})$. In this way, our thumb represents the direction of the cross-product ($ \vec{R}$) [see fig-1]. Similarly if we want the direction of $\vec{B} \times \vec{A}$; we need to put our left palm on the vector $\vec{B}$ and sweep it towards $\vec{A}$; the thumb will represent the direction of $\vec{B} \times \vec{A}$ which is $-\vec{R}$ [see fig-2]. In both cases i.e $\vec{A} \times \vec{B} = \vec{R}$ and $\vec{B} \times \vec{A} = -\vec{R}$; the thumb gives opposite direction; mathematically-

$$\vec{A} \times \vec{B} = -\vec{B} \times \vec{A}$$

Formula of Vector Product

The formula for the cross or vector product of two vectors A and B is given by –

$$\vec{A} \times \vec{B} = |\vec{A}| |\vec{B}| \sin\theta \, \hat{n}$$

and the magnitude

$$|\vec{A} \times \vec{B}| = |\vec{A}| |\vec{B}| \sin\theta$$

Where:

• $|\vec{A}|$ and $|\vec{B}|$ are the magnitude of two vector $\vec{A}$ and $\vec{B}$ respectively.
• θ is the angle $\vec{A}$ and $\vec{B}$ and $0 \leq \theta \leq 180^\circ$
• $\hat{n}$ is the unit vector perpendicular to both $\vec{A}$ and $\vec{B}$. $\hat{n}$ is determined using right-hand thumb rule.

Case-1: If the angle between $\vec{A}$ and $\vec{B}$ is 0° i.e. θ = 0°,

$$\vec{A} \times \vec{B} = |\vec{A}| |\vec{B}| \sin\theta \, \hat{n}$$

$$\vec{A} \times \vec{B} = |\vec{A}| |\vec{B}| \sin0° \, \hat{n}$$

$$\vec{A} \times \vec{B} = 0$$

vectors are parallel with the same direction.

Case-2: If the angle between $\vec{A}$ and $\vec{B}$ is 180°, i.e. θ = 180°; $\sin\theta = \sin180° = 0$

$$\vec{A} \times \vec{B} = 0$$

vectors are parallel with the opposite direction.

Case-3: If the angle between $\vec{A}$ and $\vec{B}$ is 90° i.e. θ = 90°,

$$\vec{A} \times \vec{B} = |\vec{A}| |\vec{B}| \sin90° \, \hat{n}$$

$$\vec{A} \times \vec{B} = |\vec{A}| |\vec{B}| \hat{n}$$

and the magnitude

$$|\vec{A} \times \vec{B}| = |\vec{A}| |\vec{B}|$$

If $\vec{A}$ and $\vec{B}$ represent two sides of a triangle, the area of that triangle is given by –

$$\text{Area} = \frac{1}{2} |\vec{A} \times \vec{B}|$$

Cross Product in Component Form

If $\vec{A}$ and $\vec{B}$ are two non-zero vectors and

$\vec{A} = A_x \hat{i} + A_y \hat{j} + A_z \hat{k}$

$ \vec{B} = B_x \hat{i} + B_y \hat{j} + B_z \hat{k}$

then

$$\vec{A} \times \vec{B} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ A_x & A_y & A_z \\ B_x & B_y & B_z \end{vmatrix}$$

$$= \hat{i} \begin{vmatrix} A_y & A_z \\ B_y & B_z \end{vmatrix} – \hat{k} \begin{vmatrix} A_x & A_y \\ B_x & B_y \end{vmatrix} + \hat{j} \begin{vmatrix} A_x & A_z \\ B_x & B_z \end{vmatrix}$$

For $\hat{i}$ – component

$$\begin{vmatrix} A_y & A_z \\ B_y & B_z \end{vmatrix} = (A_y B_z – A_z B_y)$$

For $\hat{j}$ – component

$$\begin{vmatrix} A_x & A_z \\ B_x & B_z \end{vmatrix} = (A_x B_z – A_z B_x)$$

For $\hat{k}$ – component

$$\begin{vmatrix} A_x & A_y \\ B_x & B_y \end{vmatrix} = (A_x B_y – A_y B_x)$$

Finally-

$\vec{A} \times \vec{B} = (A_y B_z – A_z B_y) \hat{i} – (A_x B_z – A_z B_x) \hat{j} + (A_x B_y – A_y B_x) \hat{k}$

Properties of Cross Product

Non-Commutativity Anticommutative Property: The cross product of vectors fails the commutative law. The order we perform the cross-product matters; if the order reverses the direction of the resultant vector reverses.

$$\vec{A} \times \vec{B} \neq \vec{B} \times \vec{A}$$

instead

$$\vec{A} \times \vec{B} = -(\vec{B} \times \vec{A})$$

Distributive law: The cross product is distributive over addition-

$$\vec{A} \times (\vec{B} + \vec{C}) = \vec{A} \times \vec{B} + \vec{A} \times \vec{C}$$

Scalar Multiplication: For any scalar $k$

$$k (\vec{A} \times \vec{B}) = (k \vec{A}) \times \vec{B} = \vec{A} \times (k \vec{B})$$

Cross Product of a vector with itself is zero.

$$\vec{A} \times \vec{A} = \vec{0}$$

Cross product of Orthogonal Basis Vectors: The cross product of the unit vectors $\hat{i}, \hat{j}, \hat{k}$ follows a cyclic rule. For the standard basis vectors $\hat{i}, \hat{j}, \hat{k}$ in 3 dimensions:

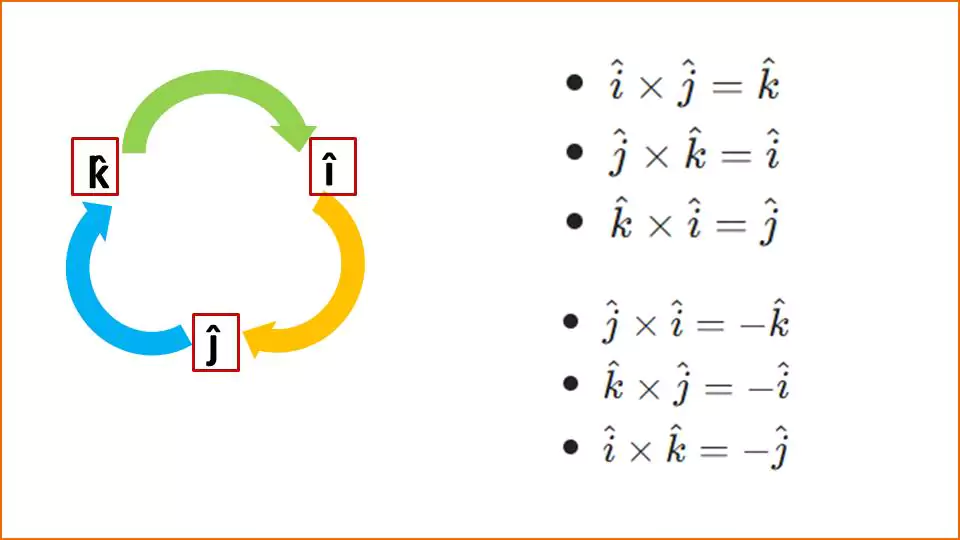
The cyclic order is

• $\hat{i} \times \hat{j} = \hat{k}$
• $ \hat{j} \times \hat{k} = \hat{i}$
• $ \hat{k} \times \hat{i} = \hat{j}$

The reverse order of the cross product gives a negative result

• $\hat{j} \times \hat{i} = -\hat{k}$
• $\hat{k} \times \hat{j} = -\hat{i}$
• $ \hat{i} \times \hat{k} = -\hat{j}$

The magnitude of $\vec{A} \times \vec{B}$ is the same as the area of a parallelogram with sides $\vec{A}$ and $\vec{B}$.

Few Solved Problems