A vector is a physical quantity that has both magnitude and direction. There are different types of vectors considered in physics and math. Among these, the unit vectors are widely used in mathematics, physics, engineering, and computer science. It represents directions independently of magnitude.
Unit Vector
A unit vector has a unit magnitude equal to 1 with a direction along that vector. A unit vector is represented by putting a “cap” or “hat” symbol (^) on a vector. For example, if $\vec{n}$ is a vector then its unit vector will be represented by $\hat{n}$.
Using scale we can construct a unit vector by setting its magnitude = 1.
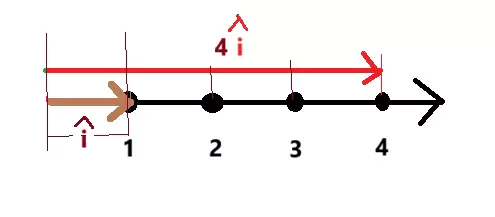
From the above figure, we see that the unit vector is $\hat{i} $ whose magnitude is = 1. And $\vec{A}$ = 4 times of unit vector $\hat{i}$.
$\therefore \vec{A} = 4\hat{i}$.
Formula of Unit Vector
If $\vec{A}$ is a vector with magnitude |$\vec{A}$|, then $\frac{\vec{A}}{|\vec{A}|}$ is a unit vector having the same direction as $\vec{A}$.
$$\therefore unit\ vector\ \hat{n}= \frac{\vec{A}}{\left| \vec{A}\right|}$$
From the above equation we can write that
$$\vec{A} = \left| \vec{A}\right|\hat{n}$$
Thus any vector ($\vec{A}$) can be represented by multiplying the magnitude of that vector ($\left| \vec{A}\right|$) with the unit vector ($\hat{n}$).
Properties of Unit Vectors
- The magnitude of a unit vector is always 1 i.e. $\left| \hat{n}\right|$ = 1.
- The unit vector is used to represent directions in space.
- A unit vector is independent of the magnitude of the original vector.
- Any vector $\vec{A}$ can be converted to a unit vector by dividing it by its magnitude.
- Unit Vector of a Zero Vector is Undefined.
- A unit vector is used in vector projections to find the scalar or component of a vector along a specific direction.
- The zero vector cannot have a unit vector because its magnitude is zero.
Unit Vectors in Cartesian Coordinate System
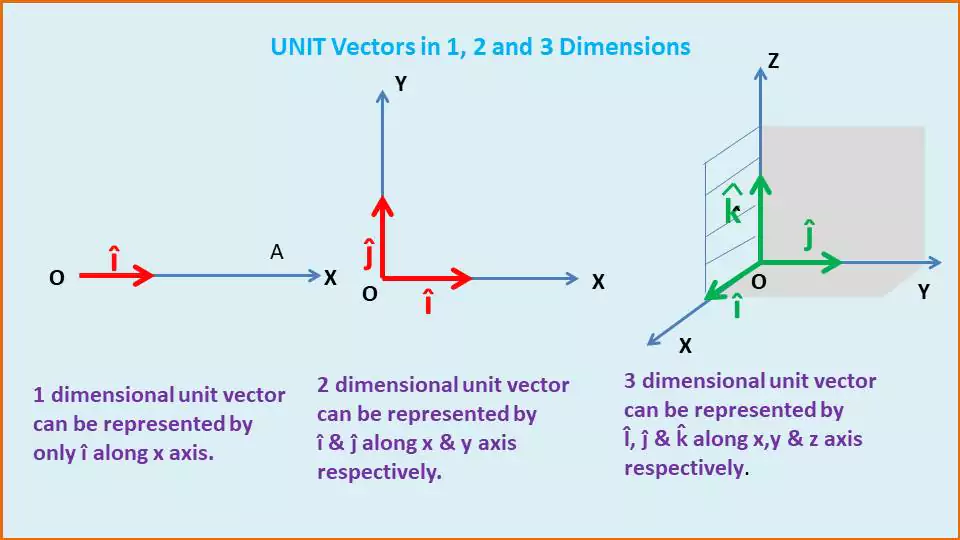
- The unit vector along x-axis is represented by $\hat{i}$ and its magnitude $\left| \hat{i}\right|=1$
- The unit vector along y-axis is represented by $\hat{j}$ and its magnitude $\left| \hat{j}\right|=1$
- The unit vector along z-axis is represented by $\hat{k}$ and its magnitude$\left| \hat{k}\right|=1$
How to find Unit Vector?
2 Dimension Cartesian Coordinate
To find a unit vector in a two-dimensional Cartesian coordinate system, we can divide a vector by its magnitude. The unit vector along the x-axis and y-axis is $\hat{i}$ and $\hat{j}$ respectively.
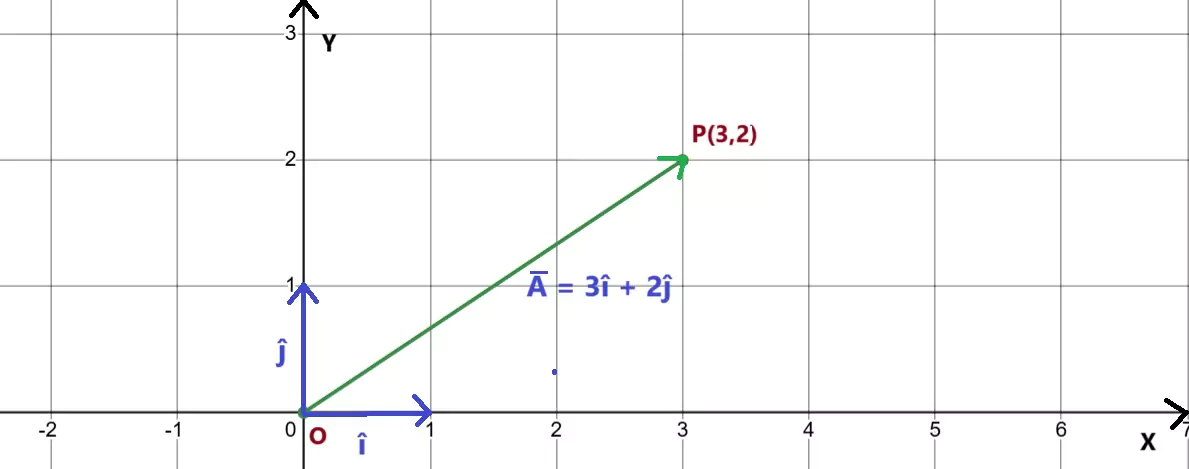
A vector $\vec{A}$ is represented by a straight line OP. It has an x component = 3 units and y component = 2 units. So the x-component is 3$\hat{i}$ and y component is 2$\hat{j}$. Thus $\vec{A} =(3,2) = 3\hat{i} + 2\hat{j}$. Its magnitude is
$\left| \vec{A}\right| = \sqrt{x^{2}+y^{2}}$.
$\left| \vec{A}\right| = \sqrt{3^{2}+2^{2}} = 3.6$.
$$\therefore unit\ vector\ \hat{a}= \frac{\vec{A}}{\left| \vec{A}\right|}$$
$$ \hat{a}= \frac{3\hat{i}+2\hat{j}}{3.6}\ along\ \vec{A}$$
3 Dimension Cartesian Coordinate
Now consider a vector $\vec{A}$ in the Cartesian coordinate system. Its position is denoted by point P(x,y,z). This means the length or the component of the vector along the x-axis is $x$, the y-axis is $y$ and the z-axis is $z$.
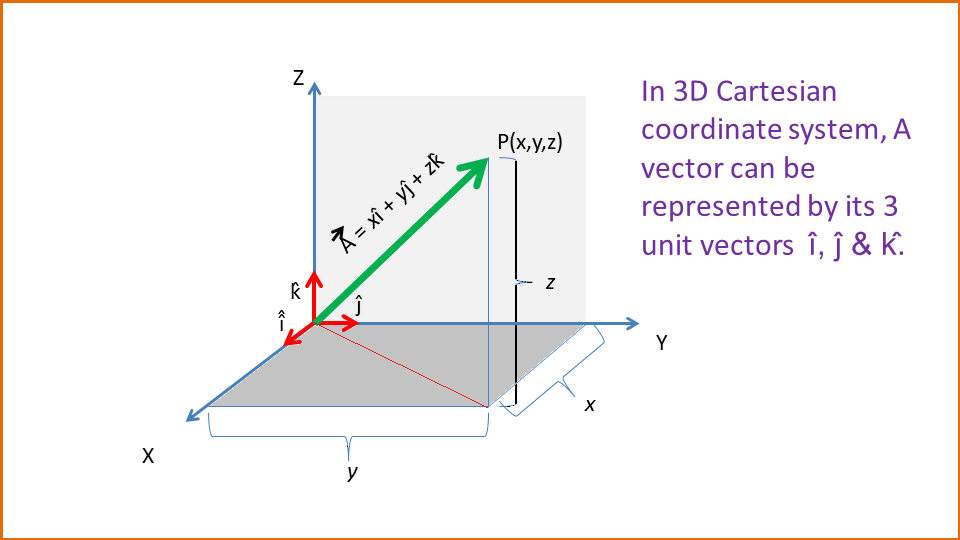
Therefore the vector $\vec{A}$ in Cartesian 3 dimension can be represented by-
$$\vec{A} = x\hat{i}+y\hat{j}+z\hat{k} $$
Now to find the unit vector of this $\vec{A}$, we first need to find the magnitude $\left| \vec{A}\right|$. $\left| \vec{A}\right|$ is given by-
$$\left| \vec{A}\right| = \sqrt{x^{2}+y^{2}+z^{2}}$$
After that, we just divide the vector $\vec{A}$ by $\left| \vec{A}\right|$. So that the unit vector is-
$$ \hat{n}= \frac{x\hat{i}+y\hat{j}+z\hat{k}} {\sqrt{x^{2}+y^{2}+z^{2}}}\ along\ \vec{A} $$
Problem: Find the unit vector in the direction of the vector $\vec{v} = \begin{bmatrix} 6 \\ 8 \end{bmatrix}$
Answer:
Given $\vec{v} = \begin{bmatrix} 6 \\ 8 \end{bmatrix} = 6\hat{i}+8\hat{j}$
We first calculate the magnitude of the vector $\vec{v}$
$\left| \vec{v}\right| = \sqrt{6^{2}+8^{2}} = \sqrt{36+64} = \sqrt{100} = 10$
Unit vector $\hat{v} =\frac{\vec{v}}{|\vec{v}|} = \frac{6\hat{i}+8\hat{j}}{10}$
$\hat{v} = \frac{6\hat{i}}{10} + \frac{8\hat{j}}{10} = 0.6\hat{i} + 0.8\hat{j}$
Verification: To confirm that $\hat{v}$ is a unit vector, we now check its magnitude:
$|\hat{v}| = \sqrt{(0.6)^2 + (0.8)^2} = \sqrt{0.36 + 0.64} = \sqrt{1} = 1$
Find the unit vector perpendicular to the vector $\vec{a} = \begin{bmatrix} 2 \\ 3 \\ -1 \end{bmatrix}$ $\vec{b} = \begin{bmatrix} -1 \\ 0 \\ 2 \end{bmatrix}$
The cross product $\vec{a}\times \vec{b}$ gives a vector perpendicular to both $\vec{a}$ and $\vec{b}$:
$$\vec{a} \times \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & 3 & -1 \\ -1 & 0 & 2 \end{vmatrix}$$
$$\vec{a} \times \vec{b} = \hat{i} \begin{vmatrix} 3 & -1 \\ 0 & 2 \end{vmatrix} – \hat{j} \begin{vmatrix} 2 & -1 \\ -1 & 2 \end{vmatrix} + \hat{k} \begin{vmatrix} 2 & 3 \\ -1 & 0 \end{vmatrix}$$
For $\hat{i}$
$$\begin{vmatrix} 3 & -1 \\ 0 & 2 \end{vmatrix} = (3)(2) – (0)(-1) = 6$$
For $\hat{j}$
$$\begin{vmatrix} 2 & -1 \\ -1 & 2 \end{vmatrix} = (2)(2) – (-1)(-1) = 4 – 1 = 3$$
For $\hat{k}$
$$\begin{vmatrix} 2 & 3 \\ -1 & 0 \end{vmatrix} = (2)(0) – (3)(-1) = 0 + 3 = 3$$
$$\therefore \vec{a} \times \vec{b} = \hat{i}(6) – \hat{j}(3) + \hat{k}(3)$$
$$\vec{a} \times \vec{b} = \begin{bmatrix} 6 \\ -3 \\ 3 \end{bmatrix}$$
$|\vec{a} \times \vec{b}| = \sqrt{6^2 + (-3)^2 + 3^2} = \sqrt{36 + 9 + 9} = \sqrt{54} = 3\sqrt{6}$
The unit vector perpendicular to $\vec{a}$ and $\vec{b}$:
$$\hat{v} = \frac{\vec{a} \times \vec{b}}{|\vec{a} \times \vec{b}|} = \frac{\begin{bmatrix} 6 \\ -3 \\ 3 \end{bmatrix}}{3\sqrt{6}}$$
$$\hat{v} = \begin{bmatrix} \frac{6}{3\sqrt{6}} \\ \frac{-3}{3\sqrt{6}} \\ \frac{3}{3\sqrt{6}} \end{bmatrix} = \begin{bmatrix} \frac{2}{\sqrt{6}} \\ \frac{-1}{\sqrt{6}} \\ \frac{1}{\sqrt{6}} \end{bmatrix}$$
$$\hat{v}= \frac{1}{3\sqrt{6}}[ 6\hat{i} – 3\hat{j} + 3\hat{k}]$$
$$\hat{v}= \frac{1}{\sqrt{6}}[ 2\hat{i} – \hat{j} + \hat{k}]$$
If $\vec{v} = \begin{bmatrix} 4 \\ -3 \end{bmatrix}$find a unit vector in the opposite direction of $\vec{v}$
At first we need to find the magnitude of $\vec{v}$
$$|\vec{v}| = \sqrt{4^2 + (-3)^2} = \sqrt{16 + 9} = \sqrt{25} = 5$$
The unit vector in the opposite direction is:
$$\hat{u} = -\frac{\vec{v}}{|\vec{v}|} = -\frac{\begin{bmatrix} 4 \\ -3 \end{bmatrix}}{5} = \begin{bmatrix} -\frac{4}{5} \\ \frac{3}{5} \end{bmatrix}$$
Final Answer:
$$\hat{u} = \begin{bmatrix} -0.8 \\ 0.6 \end{bmatrix}$$